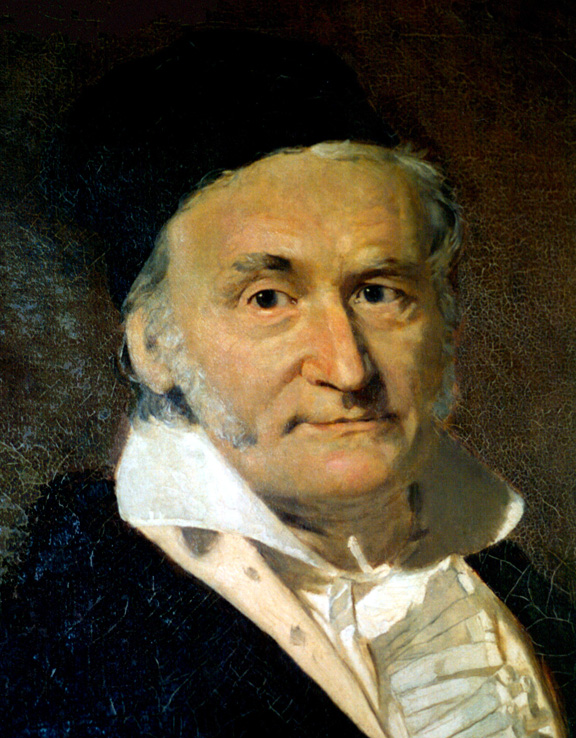Ziyaretçi
Fakir bir Alman ailenin çocuğu olan ve "Matematiğin Prensi" olarak anılan Gauss'un (1777-1855) dehası çok erken yaşlarda kendini göstermiş ve konuşmayı öğrenmeden önce toplama ve çıkarma yapmayı öğrenmiştir.
Güç koşullar altında sürdürdüğü eğitimini, 14 yaşındayken bir asilin sağladığı destekle güvence altına alabilmiştir. 16 yaşında Eukleides Geometrisi'nin alternatifi olacak yeni bir geometri tasarlamış ve 18 yaşındayken Lagrange ve Newton'un eserlerini incelemiştir.
Üniversitede öğrenciyken, sadece pergel ve cetvel kullanarak 17 kenarlı düzgün bir çokgenin çizilmesi metodunu bulmuştur. Bu buluşundan çok mutlu olmuş ve mezarının üzerine bu çokgenin oyulmasını istemiştir. Archimedes tarafından başlatılan bu geleneğin birçok matematikçiyi etkilediği anlaşılmaktadır.
Sayılar teorisi üzerine yazmış olduğu ilk büyük eseri "Disquistiones Arithmeticae" (Aritmetik Araştırmaları) ona şimdiki ününü kazandırmıştır. Eseri okuyan Lagrange, Gauss'a şunları yazmıştır: "Eseriniz sizi bir anda birinci sınıf matematikçiler arasına yükseltmiştir. Uzun zamandan beri yapılmış en güzel analitik keşfi ihtiva eden son bölümü çok önemli kabul ediyorum."
Gauss'un bu yapıtı modern sayılar teorisine temel olmuştur. Ona göre, sayılar teorisi çok önemlidir: "Matematik, bilimlerin kraliçesi olduğu gibi, sayılar teorisi de matematiğin kraliçesidir." Yeni yüzyılın ilk gününde (1 Ocak 1801) Ceres adı verilen gezegenciğin bulunması, Gauss'un astronomiye ilgisini uyandırmıştır; az sayıda gözlemden yararlanarak bu gezegenciğin yörüngesini hesaplama sorununu, Gauss, 8. dereceden bir denklem yardımıyla çözmüştür.
1802'de bulunan diğer bir gezegencik olan Pallas ile de ilgilenmiştir. İkinci eseri, bu iki gezegenciğin hareketleriyle ilgilidir. 1821 yılında Gauss, resmi bir jeodezi araştırmasına bilim danışmanı olmuş ve bu görevi ona yüzeyler ve haritacılıkla ilgili yeni teoriler ilham etmiştir.
Yıllar geçtikçe Gauss'un ilgisi matematiksel fiziğe ve karmaşık geometri araştırmalarına yönelmiştir. Bu dönemde Yer'in magnetik alanı üzerine deneysel çalışmalar yapmış ve uzaklığın karesiyle ters orantılı olarak etkileyen kuvvetler kuramını ileri sürmüştür.
1833 yılında Weber ile birlikte bir elektrik telgrafı kurmuş ve bununla düzenli mesajlar göndermiştir. Onun elektromagnetizm ile ilgili araştırmalarının 19. yüzyılda fizik biliminin gelişmesine büyük katkısı olmuştur.
Günlüklerinin ve mektuplarının ortaya çıkması, bazı önemli düşüncelerini kendisine saklamış olduğunu göstermiştir; bu belgelerden, Gauss'un 1800 gibi erken bir tarihte, eliptik fonksiyonları keşfetmiş olduğu ve 1816'da Eukleides-dışı geometriyi bildiği anlaşılmaktadır. Eukleidesçi uzay kavramının apriori (önsel) olduğunu savunan Kant'ın isabetliliğinden kuşkulanmış ve uzayın gerçek geometrisinin ancak deneyle bulunabileceğini düşünmüştür.
Gauss sadece bilimsel konularla ilgilenmemiştir; Avrupa edebiyatı, Yunan ve Roma klâsikleri, Dünya politikası, botanik ve mineroloji gibi konular da ilgi alanına girmektedir. Ana dili Almanca ile birlikte, Latince, İngilizce, Danimarkaca ve Fransızca okuyabildiği ve yazabildiği bilinmektedir; 62 yaşında bu dillere Rusça'yı da eklemeye karar vermiş ve iki yıl içinde bu dili de öğrenmiştir.
Sponsorlu Bağlantılar
Üniversitede öğrenciyken, sadece pergel ve cetvel kullanarak 17 kenarlı düzgün bir çokgenin çizilmesi metodunu bulmuştur. Bu buluşundan çok mutlu olmuş ve mezarının üzerine bu çokgenin oyulmasını istemiştir. Archimedes tarafından başlatılan bu geleneğin birçok matematikçiyi etkilediği anlaşılmaktadır.
Sayılar teorisi üzerine yazmış olduğu ilk büyük eseri "Disquistiones Arithmeticae" (Aritmetik Araştırmaları) ona şimdiki ününü kazandırmıştır. Eseri okuyan Lagrange, Gauss'a şunları yazmıştır: "Eseriniz sizi bir anda birinci sınıf matematikçiler arasına yükseltmiştir. Uzun zamandan beri yapılmış en güzel analitik keşfi ihtiva eden son bölümü çok önemli kabul ediyorum."
Gauss'un bu yapıtı modern sayılar teorisine temel olmuştur. Ona göre, sayılar teorisi çok önemlidir: "Matematik, bilimlerin kraliçesi olduğu gibi, sayılar teorisi de matematiğin kraliçesidir." Yeni yüzyılın ilk gününde (1 Ocak 1801) Ceres adı verilen gezegenciğin bulunması, Gauss'un astronomiye ilgisini uyandırmıştır; az sayıda gözlemden yararlanarak bu gezegenciğin yörüngesini hesaplama sorununu, Gauss, 8. dereceden bir denklem yardımıyla çözmüştür.
1802'de bulunan diğer bir gezegencik olan Pallas ile de ilgilenmiştir. İkinci eseri, bu iki gezegenciğin hareketleriyle ilgilidir. 1821 yılında Gauss, resmi bir jeodezi araştırmasına bilim danışmanı olmuş ve bu görevi ona yüzeyler ve haritacılıkla ilgili yeni teoriler ilham etmiştir.
Yıllar geçtikçe Gauss'un ilgisi matematiksel fiziğe ve karmaşık geometri araştırmalarına yönelmiştir. Bu dönemde Yer'in magnetik alanı üzerine deneysel çalışmalar yapmış ve uzaklığın karesiyle ters orantılı olarak etkileyen kuvvetler kuramını ileri sürmüştür.
1833 yılında Weber ile birlikte bir elektrik telgrafı kurmuş ve bununla düzenli mesajlar göndermiştir. Onun elektromagnetizm ile ilgili araştırmalarının 19. yüzyılda fizik biliminin gelişmesine büyük katkısı olmuştur.
Günlüklerinin ve mektuplarının ortaya çıkması, bazı önemli düşüncelerini kendisine saklamış olduğunu göstermiştir; bu belgelerden, Gauss'un 1800 gibi erken bir tarihte, eliptik fonksiyonları keşfetmiş olduğu ve 1816'da Eukleides-dışı geometriyi bildiği anlaşılmaktadır. Eukleidesçi uzay kavramının apriori (önsel) olduğunu savunan Kant'ın isabetliliğinden kuşkulanmış ve uzayın gerçek geometrisinin ancak deneyle bulunabileceğini düşünmüştür.
Gauss sadece bilimsel konularla ilgilenmemiştir; Avrupa edebiyatı, Yunan ve Roma klâsikleri, Dünya politikası, botanik ve mineroloji gibi konular da ilgi alanına girmektedir. Ana dili Almanca ile birlikte, Latince, İngilizce, Danimarkaca ve Fransızca okuyabildiği ve yazabildiği bilinmektedir; 62 yaşında bu dillere Rusça'yı da eklemeye karar vermiş ve iki yıl içinde bu dili de öğrenmiştir.
Biyografi Konusu: Carl Friedrich Gauss nereli hayatı kimdir.

 Carl Friedrich Gauss
Carl Friedrich Gauss