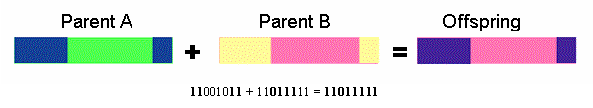Genetik Algoritmalar

Genetik Algoritmalar

Genel Bilgiler

Sponsorlu Bağlantılar

Modern bilimde veri kümeleri arasındaki ilişkileri, tecrübelerden de faydalanarak belirlemek, üzerinde çokça çalışılan ve araştırılan bir taslaktır. Günümüzdeki araştırma konuları ve problemleri eskiye nazaran çok daha karışıktır. Bu karışıklık problemi etkileyen parametre sayısının fazlalığından ve problemin çözüm kümesinin boyutunun büyümesinden kaynaklanmaktadır. Bundan dolayı elinizdeki verilerin analizi ve sonucu bu verilerden kestirme yöntemlerinin önemi araştırmacılar için gittikçe artmaktadır. Faydalı iyi bir veri analiz yöntemi şu kriterlere göre değerlendirilebilir. İyi tahmin veya sonucu kestirmeye yönelik olmalı, sistemin içindeki her bir mekanizmanın analiz edilebilmesi ve sonuçların mümkün olabilecek çözüm uzayı kümesinde olmasıdır. Bu tür problemlerdeki çözüm kümesinin büyüklüğü bir taraftan elde edilen çözümün değerlendirilmesinde zorluk çıkarırken diğer taraftan lineer yöntemlerin uygulanmasını imkansız kılacaktır.
Geçmişte araştırmacılar tarafından çalışılan, parametreler arasındaki ilişkiler, genelde deneme yoluyla, zor olan örneklerde karmaşık veya sabit olmayan ilişkiler için yapılmış; fakat parametre sayısı artınca çözümsüzlük veya elde edilen çözümü değerlendirememe problemini getirmiştir. İstatistiksel yöntemler, araştırmacılara ilişkileri bulmada faydalı olan ilk araçlardandır. İstatistiksel yöntemlerde:

1) Verinin normal toplandığı,
2) Verinin eşitlik ilişkisinin belirli bir formda olması (ör: lineer, quadratic, veya polinomsal),
3) Değişkenlerin bağımsız olması gerekir.

Eğer problem bu kriterleri sağlarsa, istatistiksel yöntem ilişkileri bulmada faydalı olabilir. Oysa gerçek hayatta problemler bu kriterleri nadiren sağlarlar.
Modern sonuç kestirme veya sonuç geliştirme algoritmaları bu kriterlerle sınırlandırılamazlar. Neural network (Yapay sinir ağları) veya Artificial intelligence (Yapay zeka) teknikleri karmaşık ilişkileri kapsamayabilir; fakat mekanizmanın önemli ilişkilerini tanımlayabilen güçlü tahmin modelleridir. Buna rağmen, diğer bir teknik Genetik Algoritma ve Genetik Programlama teknikleri çok daha güçlüdürler ve karışık çözüm uzayını daha da geniş bulabilirler. Bağımsız olan veri ve parametreler ile mekanizmanın ilişkilerini bulmada başarılı örnekleri vardır.
Genetik Algoritma, biyolojik bir sistemin, çevresine adaptasyonunda kullandığı metodun örneklendirilmesidir. Bilgisayarda, bu tür çok parametreli optimum bulma problemlerine ve makine öğrenme problemlerine çözüm modeli olarak alınabilir.
Doğal adaptasyondan esinlenen GA’ nın basit olarak iskeleti:

a) Bireyin bulunduğu ortamda hayatta kalmak için, kendi kendisini değiştirerek ortama uygun hale gelmesi,
b) Bu adaptasyon boyunca, yeni üretilecek nesillere, bu özellikler ile birlikte mümkün olabilecek daha çok değişim aktarılarak, bireylerin daha çok uyumlu hale getirilmesi olarak özetlenebilir.

Mühendislikte, bilimde, ekonomide, finansmanda v.s. deki problemleri çözmede kullanılan arama teknikleri, hesap-temelli ve direkt arama teknikleri olarak sınıflandırılabilir. Eğer problemler sayısal veya analitik olarak iyi tanımlanabiliyorsa veya çözüm uzayı küçük ve tek ise, hesap temelli arama tekniği daha iyi çalışır. Buna rağmen hesap-temelli teknik mühendislik optimizasyoların da gittikçe artan optimum bulma fonksiyonlarında oldukça zayıf kalır. Sadece fonksiyon bilgisi gerekli olan Doğrudan arama tekniği, hesap-temelli teknikten daha kısa sürede işler ve daha etkilidir. Doğrudan arama tekniğinin esas problemi, ulaşılabilen bilgisayar zamanı ile optimal çözümün kesinliği arasındaki bağıntıdır (Genetic Algorithms in Search, Optimization, and Machine Learning, Goldberg, 1989).

Genetik Algoritmanın Tarihçesi

Michigan Üniversitesinde psikoloji ve bilgisayar bilimi uzmanı olan John Holland bu konuda ilk çalışmaları yapan kişidir. Mekanik öğrenme (machine learning) konusunda çalışan Holland, Darwin’in evrim kuramında etkilenerek canlılarda yaşanan genetik süreci bilgisayar ortamında gerçekleştirmeyi düşündü. Tek bir mekanik yapının öğrenme yeteneğini geliştirmek yerine böyle yapılarda oluşan bir topluluğun çoğalma, çiftleşme, mutasyon, vb. genetik süreçlerden geçerek başarılı (öğrenebilen) yeni bireyler oluşturabildiğini gördü. Araştırmalarını, arama ve optimumu bulma için, doğal seçme ve genetik evrimden yola çıkarak yapmıştır. İşlem boyunca, biyolojik sistemde bireyin bulunduğu çevreye uyum sağlayıp daha uygun hale gelmesi örnek alınarak, optimum bulma ve makine öğrenme problemlerinde, bilgisayar yazılımı modellenmiştir.
Çalışmalarının sonucunu açıkladığını kitabının 1975’te yayınlanmasından sonra geliştirdiği yöntemin adı Genetik Algoritmalar (ya da kısaca GA) olarak yerleşti. Ancak 1985 yılında Holland’ın öğrencisi olarak doktorasını veren David E. Goldberg adlı inşaat mühendisi 1989 da konusunda bir klasik sayılan kitabını yayınlayana dek genetik algoritmaların pek pratik yararı olmayan bir araştırma konusu olduğu düşünülüyordu. İlk olarak Hollanda’ da makine öğrenme sistemlerine yardımcı olarak kullanılmış daha sonra De Jong Goldberg ve diğerleri tarafından analiz edilmiştir. Goldberg, GA’nın çok sayıda kollara ayrılmış gaz borularında, gaz akışını düzenlemek ve kontrol etmek için uygulamasını tanımlamıştır. Ayrıca kendisinin kullandığı makine öğrenmesi, nesne tanıma, görüntü işleme ve işlemsel arama gibi alanlarda kullanıldığını vurgulamıştır.
Goldberg’in gaz boru hatlarının denetimi üzerine yaptığı doktora tezi ona sadece 1985 National Science Foundation Genç Araştırmacı ödülünü kazandırmakla kalmadı, genetik algoritmaların pratik kullanımının da olabilirliğini kanıtladı. Ayrıca kitabında genetik algoritmalara dayalı tam 83 uygulamaya yer vererek GA’nın dünyanın her yerinde çeşitli konularda kullanılmakta olduğunu gösterdi.

Kuramsal Temeller

Genetik Algoritmanın Tanımı

Genetik algoritma, doğadaki evrim mekanizmasını örnek alan bir arama metodudur ve bir veri grubundan özel bir veriyi bulmak için kullanılır. Genetik algoritmalar 1970’lerin başında John Holland tarafından ortaya atılmıştır. Genetik Algoritmalar, Evrimsel Genetik ve Darwin’in Doğal seleksiyonuna benzerlik kurularak geliştirilmiş “iteratif ”, ihtimali bir arama metodudur.
Genetik algoritmalar doğada geçerli olan en iyinin yaşaması kuralına dayanarak sürekli iyileşen çözümler üretir. Bunun için “iyi”nin ne olduğunu belirleyen bir uygunluk (fitness) fonksiyonu ve yeni çözümler üretmek için yeniden kopyalamadeğiştirme (mutation) gibi operatörleri kullanır. Genetik algoritmaların bir diğer önemli özelliği de bir grup çözümle uğraşmasıdır. Bu sayede çok sayıda çözümün içinden iyileri seçilip kötüleri elenebilir.
Genetik algoritmaları diğer algoritmalardan ayıran en önemli özelliklerden biri de seçmedir. Genetik algoritmalarda çözümün uygunluğu onun seçilme şansını arttırır ancak bunu garanti etmez. Seçim de ilk grubun oluşturulması gibi rasgeledir ancak bu rasgele seçimde seçilme olasılıklarını çözümlerin uygunluğu belirler.
Genetik Algoritmaları (GA) diğer metodlardan ayıran noktalar şu şekilde sıralanabilir:
(recombination),

• GA , sadece bir arama noktası değil , bir grup arama noktası (adaylar ) üzerinde çalışır. Yani arama uzayında , yerel değil global arama yaparak sonuca ulaşmaya çalışır. Bir tek yerden değil bir grup çözüm içinden arama yapar.
• GA , arama uzayında bireylerin uygunluk değerini bulmak için sadece “amaç - uygunluk fonksiyonu” (objective-fitness function ) ister. Böylelikle sonuca ulaşmak için türev ve diferansiyel işlemler gibi başka bilgi ve kabul kullanmaya gerek duymaz.
• Bireyleri seçme ve birleştirme aşamalarında deterministik kurallar değil “ olasılık kuralları” kullanır.
• Diğer metodlarda olduğu gibi doğrudan parametreler üzerinde çalışmaz. Genetik Algoritmalar, optimize edilecek parametreleri kodlar ve parametreler üzerinde değil, bu kodlar üzerinde işlem yapar. Parametrelerin kodlarıyla uğraşır. Bu kodlamanın amacı, orjinal optimizasyon problemini kombinezonsal bir probleme çevirmektir.
• Genetik algoritma ne yaptığı konusunda bilgi içermez, nasıl yaptığını bilir. Bu nedenle kör bir arama metotudur.
• Olasılık kurallarına göre çalışırlar. Programın ne kadar iyi çalıştığı önceden kesin olarak belirlenemez. Ama olasıklıkla hesaplanabilir.
• GA, kombinezonsal bir atama mekanizmasıdır.

Genetik Algoritmalar, yeni bir nesil oluşturabilmek için 3 aşamadan geçer:

1. Eski nesildeki her bir bireyin uygunluk değerini hesaplama.
2. Bireyleri, uygunluk değerini göz önüne alarak (uygunluk fonksiyonu ) kullanılarak seçme.
3. Şeçilen bireyleri, çaprazlama (crossover), mutasyon (mutation) gibi genetik operatörler kullanarak uyuşturma.

Algoritmik bakış açısından bu aşamalar, mevcut çözümleri lokal olarak değiştirip birleştirmek olarak görülebilir.
Genetik Algoritmalar; başlangıçta bilinmeyen bir arama uzayından topladığı bilgileri yığıp, daha sonraki aramaları alt arama uzaylarına yönlendirmek için kullanılır.

Kodlama Yöntemleri

Kodlama planı Genetik algoritmanın önemli bir kısmını teşkil eder. Çünkü bu plan bilginin çerçevesini şiddetle sınırlayabilir. Öyle ki probleme özgü bilginin bir kromozomsal gösterimiyle temsili sağlanır. Kromozom genellikle, problemdeki değişkenlerin belli bir düzende sıralanmasıdır. Kromozomu oluşturmak için sıralanmış her bir değişkene “gen” adı verilir. Buna göre bir gen kendi başına anlamlı genetik bilgiyi taşıyan en küçük genetik yapıdır. Mesela; 101 bit dizisi bir noktanın x-koordinatının ikilik düzende kodlandığı gen olabilir. Aynı şekilde bir kromozom ise Bir ya da daha fazla genin bir araya gelmesiyle oluşan ve problemin çözümü için gerekli tüm bilgiyi üzerinde taşıyan genetik yapı olarak tanımlanabilir. Örnek vermek gerekirse; 100011101111 x1, y1, x2, y2 koordinatlarından oluşan iki noktanın konumu hakkında bize bilgi verecektir.
Bu parametreleri kodlarken dikkat edilmesi gereken en önemli noktalardan biri ise kodlamanın nasıl yapıldığıdır. Örnek olarak kimi zaman bir parametrenin doğrusal ya da logaritmik kodlanması GA performansında önemli farka yol açar.
Kodlamanın diğer önemli bir hususu ise kodlama gösteriminin nasıl yapıldığıdır. Bu da yeterince açık olmamakla birlikte GA performansını etkileyen bir noktadır. Bu konu sonradan anlatılacaktır.

Uygunluk Teknikleri

Başlangıç topluluğu bir kez oluşturulduktan sonra evrim başlar. Genetik algoritma bireylerin uygunluk ve iyiliklerine göre ayrılıp fark edilmesine gerek duyar. Uygunluk, topluluktaki bir kısım bireyin problemi nasıl çözeceği için iyi bir ölçüdür. O problem parametrelerini kodlamayla ölçülür ve uygunluk fonksiyonuna giriş olarak kullanılır. Yüksek ihtimalle uygun olan bu üyeler tekrar üreme, çaprazlama ve mutasyon operatörleriyle seçilirler.
Bazı problemler için bireyin uygunluğu, bireyden elde edilen sonuç ile tahmin edilen sonuç arasındaki hatadan bulunabilir. Daha iyi bireylerde bu hata sıfıra yakın olur. Bu hata genellikle, girişin tekrar sunulacak kombinezonlarının ortalaması veya toplamıyla hesaplanır (değerler değişkenlerden bağımsızdır). Beklenen ve üretilen değer arasındaki korelasyon etkeni, uygunluk değerini hesaplamak için kullanılabilir. (Koza 1994).
Objektif fonksiyonu (Değerlendirme fonksiyonu) her bir kromozomun durumunu değerlendirmek için mekanizmayı sağlayan ana bir kaynaktır. Bu GA ve sistem arasında önemli bir bağlantıdır. Fonksiyon giriş olarak kodu çözülmüş şekilde kromozom (Phenotype) alır ve kromozomun performansına bir ölçü olarak bir objektif değer üretir. Bu diğer kromozomlar için de yapıldıktan sonra yapıldıktan sonra bu değerler kullanılarak, uygun değerler uygunluk fonksiyonuyla hesaplanıp belli bir düzende planlanır. Bu planlamayı sağlayan ve uygunluk teknikleri olarak bilinen birçok yöntem vardır. Çoğu ortak kullanılan bu yöntemler şunlardır:

1. Pencereleme

Populasyonda en kötü kromozomun objektif değerinin Vw olduğunu kabul edersek her bir kromozomun i ve en kötü kromozomu arasında farkla orantılı bir uygunluk değeri fi atanabilir. Bu durum matematiksel olarak şu şekilde ifade edilebilir:
Burada Vi kromozom i ‘nin objektif değeri ve c ise uygunluğun negatif çıkmamasını sağlayacak kadar büyük bir sayıdır. Eğer bir maksimizasyon problemiyle karşılaşılırsa denklemde pozitif işaret kabul edilir. Diğer yandan minimizasyon gerekliyse negatif işaret kabul edilir.

2. Lineer Normalizasyon

Objektif fonksiyonun maksimize veya minimize durumuna göre kromozomlar objektif değerin artma veya azalma düzenine göre sıralanır. En iyi kromozoma rastgele en iyi bir uygunluk fbest atanarak sıralanmış düzende diğer kromozomların uyguluğu lineer bir fonksiyonla bulunur:


Burada d eksilme oranıdır. Bu teknik populasyonun ortalama objektif değerini ortalama uygunluk içerisinde ayrıntılarıyla planlamayı sağlar.
Bu iki teknikten başka kullanıcının kendisinin belirleyeceği başka yöntemler de mevcuttur.

Genetik Operatörler

Kullanılan genetik operatörler, varolan nesil (population) üzerine uygulanan işlemlerdir. Bu işlemlerin amacı, daha iyi özelliğe sahip yeni nesiller üretmek ve arama algoritmasının alanını genişletmektir.
3 tip genetik operatör vardır:

1. Seleksiyon (Selection / Reproduction)
2. Çaprazlama (Crossover)
3. Mutasyon (Mutation)

1. Seleksiyon (Selection / Reproduction)

Yeniden üretme operatörü, hazır topluluktan uygun olan bireylerin seçilmesi ve bunların sonraki topluluğa kopyalanarak hayatta kalmalarıyla ilgilidir. Seçim modeli, tabiatın hayatta kalabilmek için uygunluk mekanizması modelidir. Yeniden üretme işleminde, bireyler onların uygunluk fonksiyonlarına göre kopya edilirler. Uygunluk fonksiyonu, mümkün olduğu kadar yükseltilmesi gereken bazı faydalı ve iyi ölçülerdir. Topluluk uzayındaki her bir bireyin uygunlukları baz alınarak ne kadar sayıda kopyasının olacağına karar verilir. En iyi bireylerden daha fazla kopya alınır, en kötü bireylerden kopya alınmaz. Bu hayatta kalmak için uygunluk stratejisinin GA ya sağladığı avantajdır.

1.1. Rulet Tekerleği Seçimi

GA tarafından üretilen döllerin sayısını belirlemede birkaç yol vardır. Birbirine yakın parametrelerden kaçınmak için uygun bir seçim metodu kullanılmalıdır. Tekrar üretme başlangıcında basit bir yöntem “roulette wheel selection” (rulet tekerleğiyle seçim)'e göre bireylerin uygunluk değerlerini bir rulet tekerleğinde hazırlar. Rasgele tekerleğin döndürülmesinden sonra, bireyin bir sonraki nesil için seçilmesi, tekerlek üzerinde kapladığı alanla doğrudan bağlantılıdır. Bu yöntem düşük uygunluğa sahip bireylere de seçilme hakkı verir.

Fi: i. Eleman için uygunluk değeri
N: Birey sayısı

Ebeveynler uygunluklarına göre seçilirler. Kromozomlar ne kadar iyiyse, o kadar seçilme şansları fazladır. Şöyle bir rulet tekerleği düşünün.

Sonra bir bilye atılır ve kromozomu seçer. Daha fazla uygunluğu olan kromozomlar daha çok seçilecektir. Bu aşağıdaki algoritmayla simule edilebilir:
1. [Sum] Populasyondaki tüm kromozom uygunlukları toplamını hesapla – toplam S.
2. [Select] (0,S) – r aralığından rastgele bir sayı üret.
3. [Loop] Populasyon boyunca git ve uygunlukları 0’dan toplam s ‘e kadar topla. Eğer toplam s , r ‘den büyükse dur ve olduğun yerdeki kromozomu geri gönder.
Tabii ki 1. basamak her populasyon için bir kez performe edilir.

1.2 Rank Seçimi

Yukarıdaki seçim eğer uygunluklar çok fazla değişiyorsa bazı problemlere yol açacaktır. Mesela en iyi kromozom uygunluğu tüm rulet tekerleğinin %90’ı ise diğer kromozomların seçilme şansları çok az olacaktır. Rank seçimi önce populasyonu sıralar ve daha sonra her kromozom uygunluğu bu sıralamadan sonra alır. En kötüsü 1 uygunluğunu alacak, ikinci en kötü 2 ve en iyisi N uygunluk değerini alacak ki N de populasyondaki kromozom sayısıdır.
Sayıları düzenlemek için uygunlukları değiştirdikten sonra durumun nasıl değiştiğini aşağıdaki şekilde görebilirsiniz:

Bundan sonra her kromozomun seçilme hakkı olacaktır. Fakat bu metod daha yavaş gibidir, çünkü en iyi kromozomlar diğerlerinden fazla değişiklik göstermez.

1.3 Steady-State Seçimi (Kararlı Hal)

Bu yerine geçme yöntemleri olarak da adlandırılabilirler. Bu ebeveynleri seçmek için kısmi bir metod değildir. Bu seçimin ana fikri kromozomların büyük kısmı bir sonraki nesilde hayatta kalmak zorundadır.
O zaman GA şu şekilde çalışır. Yeni çocuklar oluşturmak için her nesilde güzel iyi uygunluklu birkaç kromozom seçilir. Sonra kötü düşük uygunluklu bazı kromozomlar atılır ve yeni çocuk onun yerine yerleştirilir. Populasyonun geri kalan kısmı yeni nesilde hayattadır. Yani kısaca bu yöntemde alt populasyon oluşturulduktan sonra uygunluklar hesaplanır, en kötü kromozomlar yerlerini başlangıç populasyonundaki en iyi kromozomlara terk eder.

1.4 Elitizm

Bu da yerine geçme metodu olarak bilinir. Elitizm fikriyle zaten daha önce tanışılmıştı. Mutasyon ve çaprazlamalarla yeni nesil oluştururken en iyi kromozomu seçmek için büyük bir şansa sahip oluruz.
Elitizm en iyi kromozomu ya da birkaç en iyi kromozomları yeni nesile kopyalama metodunun adıdır. Gerisi klasik yolla yapılır. Elitizm çok hızlı bir şekilde GA’ nın performansını arttırır çünkü en iyi bulunan çözümü kaybetmeyi önler.
Ayrıca Musbaka ve Oranlama yöntemleri de vardır.

2. Çaprazlama (Crossover)

Amaç, ana (parent) kromozom genlerinin yerini değiştirerek çocuk (child) kromozomlar üretmek ve böylece varolan uygunluk değeri yüksek olan kromozomlardan, uygunluk değeri daha yüksek olan kromozomlar elde etmektir. Burada önemli olan bir konuda , çaprazlama noktasının çaprazlamadan elde edilecek çocuk kromozomların uygunluk değerleri üzerindeki etkisidir. Bu işlem yapılırken her zaman sonuçlar önceden tahmin edilemez. Bu yüzden gelişigüzel yapılan değişikliklerde sonucun mükemmelliğe doğru gitmesi için belirli kriterler bulmak için çalışılır. Kromozomlardaki genlerin yapısı ve etkileri araştırılarak, bu genlere yapılan müdahalelerle bireye bazı iyi özellikler kazandırılabilir. Çaprazlamadan elde edilecek çocuk kromozomların uygunluk değeri bir önceki ana kromozomlardan daha yüksek olmayabilir.
Tablo 1.'de biyolojik çaprazlamaya bir örnek verilmiştir:

Benzer şekilde GA, çaprazlama işlemini uygunluk değerlerine göre seçilmiş iki ebeveyn bireyden, iyi özellikte yeni bireyler elde etmek için kullanır. Çaprazlama rasgele seçilmiş iki çift katarın içindeki alt küme bilgilerin değiştirilmesi işlemdir. Kendi içindeki bilgilerini 1. Pozisyondan itibaren, katarın uzunluğunun bir eksik pozisyonuna kadar, aradaki bilgi kısmen karşılıklı bireyler arasında yer değiştirilir.
Eğer iki bireyin problemin çözümünde bazı etkileri var ise onların bir parçaları faydalı, iyi veya uygun nitelenebilecek bilgi taşımaktadır. Çaprazlama belki problemin çözümünde, bu faydalı bilgileri birleştirerek, daha çok etkili yeni bireyler üretecektir. Tablo 2.'de ikili kodda verilmiş bir katarda, örnek 2 bitlik bir çaprazlama işlemi verilmiştir.


Çaprazlamadan başka tersinme denilen bir üreme yöntemi daha vardır. Holland bunu tanımlayarak kromozom uzunluğu çok olan bireylerde çaprazlama yerine bunun kullanılmasını performans açısından önermiştir. Tersinme (inversion) bir kromozomu oluşturan genlerden ardışık bir grubun kendi içerisinde birbirleriyle yer değiştirerek ters dizilmeleridir. Örneğin:011110101 kromozomu (her genin bir bit olduğu varsayımı ile) 5. ve 8. Gen kromozomları arasında tersindiğinde ortaya 011101011 kromozomu çıkar.
Tersinme genellikle kromozom uzunluğu fazla olan populasyonlara uygulanır.

3. Mutasyon (Mutation)

Amaç, varolan bir kromozomun genlerinin bir ya da birkaçının yerlerini değiştirerek yeni kromozom oluşturmaktır. Yeniden ve sürekli yeni nesil üretimi sonucunda belirli bir süre sonra nesildeki kromozomlar birbirlerini tekrarlama konumuna gelebilir ve bunun sonucunda farklı kromozom üretimi durabilir veya çok azalabilir. İşte bu nedenle nesildeki kromozomlarının çeşitliğini artırmak için kromozomlardan bazıları mutasyona uğratılır. Açıklandığı gibi mutasyonun birinci maksadı bir populasyonun içindeki değişimi tanımlamaktır. Mutasyon populasyonlarda çok önemlidir. Öyle ki burada ilk populasyon mümkün olan tüm alt çözümlerin küçük bir alt kümesi olabilir ve ilk populasyondaki tüm kromozomların önemli biti sıfır olabilir. Halbuki o bitin problemin çözümü için 1 olması gerekebilir ve bunu da çaprazlama düzeltemeyebilir. Bu durumda o bit için mutasyon kaçınılmazdır. Genellikle önerilen mutasyon oranı 0.005/bit/generasyondur. Bu işlem çaprazlamadan sonra gelir. Mutasyonun yapılıp yapılmayacağını bir olasılık testi belirler. Örneğin yeni neslin ortalama uygunluğu £ Eski neslin ortalama uygunluğu ise; x. Kromozomun y. Bitini değiştir denilebilir. Bu yeni çocuğu rast gele değiştirir. İkili kodlama için rast gele seçilmiş bitlerden 0’ları 1, 1’leri 0 yaparız.
Tablo 3. bit katarında hazırlanmış bir mutasyon operatörünü göstermektedir:

Genetik Algoritmaların Çalışma Prensibi

Genetik algoritmanın çalışmasını şöyle özetleyebiliriz:


İşlemleri adım adım açıklamak gerekirse:

Adım-1.
Bu adıma toplumda bulunacak birey sayısını belirleyerek başlanmaktadır. Kullanılacak sayı için bir standart yoktur. Genel olarak önerilen 100-300 aralığında bir büyüklüktür. Büyüklük seçiminde yapılan işlemlerin karmaşıklığı ve aramanın derinliği önemlidir. Toplum bu işlemden sonra rasgele oluşturulur.Kromozomun temsil ettiği çözüm hakkında bilgiyi herhangi bir yollla içermesi gerekir. En çok kullanılan kodlama ikili stringtir.

Tablo 2. İkili kodlama

Her kromozom bir ikili stringe sahiptir. Bu stringteki her bit çözümün belli karakteristiğini temsil eder, veya tüm string bir sayıyı temsil eder. Tabiki bir çok kodlama yolu vardır. Bu daha çok çözülen probleme bağlıdır. Mesela tam sayı veya reel sayı olarak kodlanabilir, bazen de bazı permutasyonları kodlamak kullanışlı olabilir.

1. Permutasyon kodlama

Düzenleme problemlerinde kullanılır. Satıcı gezici problemi veya Task Ordering Probleminde. Burada her kromozom sayıları bir sırada temsil eden bir sayılar stringidir.

Tablo 3. Permutasyon kodlamalı kromozom örnekleri

Permutasyon kodlama sadece ordering problemleri için kullanışlıdır.

2. Değer kodlama

Reel sayılar gibi komplike değerlerin kullanıldığı problemlerde direk değer kodlanması kullanılabilir. Bu tip problemler için ikili kodlama işi çok zordur.

Bu bazı özel problemler için çok iyidir. Diğer taraftan bu tip kodlama için probleme özel yeni bazı mutasyon ve çaprazlamalar geliştirmek lazımdır.

3. Ağaç kodlama

Bu, gelişen değişen programlar veya ifadeler için kullanılır (Genetik programlama). Ağaç kodlamada her her kromozom bazı nesnelerin, mesela fonksiyonlar ya da programlama dilindeki komutlar gibi, bir ağacıdır şeklinde verilebilir.

LISP programlama dili bunu çok kullanır

Adım-2.
Kromozomların ne kadar iyi olduğunu bulan fonksiyona uygunlukfonksiyonu denir. Bu fonksiyon işletilerek kromozomların uygunluklarının bulunmasına ise hesaplama (evaluation) adı verilir. Bu fonksiyon genetik algoritmanın beynini oluşturmaktadır. Genetik algoritmada probleme özel çalışan tek kısım bu fonksiyondur. Uygunluk fonksiyonu kromozomları problemin parametreleri haline getirerek onların bir bakıma şifresini çözmektedir (decoding), sonra bu parametrelere göre hesaplamayı yaparak kromozomların uygunluğunu bulur. Çoğu zaman genetik algoritmanın başarısı bu fonksiyonun verimli ve hassas olmasına bağlı olmaktadır.

Adım-3.
Kromozomların eşlenmesi kromozomların uygunluk değerlerine göre yapılır. Bu seçimi yapmak için rulet tekerleği seçimi (roulette wheel selection) , turnuva seçimi (Tournament Selection) gibi seçme yöntemleri vardır. Örnek olarak bu çalışmada kullanılan rulet tekerleği seçimi aşağıda açıklanmıştır:

1- Tüm bireylerin uygunluk değerleri bir tabloya yazılır.
2- Bu değerler toplanır.
3- Tüm bireylerin uygunluk değerleri toplama bölünerek [0,1] aralığında sayılar elde edilir. Bu sayılar bireylerin seçilme olasılıklarıdır. Sayıların hepsi bir tabloda tutulur.
4- Seçilme olasılıklarını tuttuğumuz tablodaki sayılar birbirine eklenerek rasgele bir sayıya kadar ilerlenir. Bu sayıya ulaşıldığında yada geçildiğinde son eklenen sayının ait olduğu çözüm seçilmiş olur.

Bu yönteme rulet tekerleği seçimi ismi, bir daireyi, çözümlerin uygunluklarına göre dilimleyip çevirdiğimizde olacakların benzeşimi olduğu için verilmiştir.
Rulet tekerleği seçimi çözümlerin uygunluk değerlerinin negatif olmamasını gerektirir. Çünkü olasılıklar negatif olursa bu çözümlerin seçilme şansı yoktur. Çoğunluğunun uygunluk değeri negatif olan bir toplumda yeni nesiller belli noktalara takılıp kalabilir.

İkili kodlamada çaprazlama

Gen takası (crossover) genetik algoritmanın motoru kabul edilir. Basitçe olay iki ebeveyn kromozomun arasında belirlenen parçaların takasıdır.
Tek noktalı İki noktalı
Düzenli
Aritmetik

İkili kodlamada mutasyon

Permutasyon kodlamada çaprazlama

Tek noktalı çaprazlamada bir nokta seçilir ilk ebeveynden bu permutasyonun kopyalandığı noktaya kadar,sonra ikinci ebeveyn okunur ve sayı çocukta hala yoksa o eklenir.

Permutasyon kodlamada mutasyon

Değer kodlamada çaprazlama
İkili kodlamadaki tüm çaprazlamalar kullanılabilir.

Değer kodlamada mutasyon
Reel değer kodlama için seçilen değere küçük bir sayı eklenir ya da çıkarılır.

Ağaç kodlamada çaprazlama

Seçilen düğümler değiştirilir. Operatorlar sayılar değiştirilir. Gen takası toplumda çeşitliliği sağlar. İyi özelliklerin bir araya gelmesini kolaylaştırarak en iyiye yaklaşmayı sağlar. Değiştirme kromozomun bir parçasının dışarıdan değiştirilmesi şeklinde tanımlanır. Değiştirme görünüşte genetik algoritmanın dayanak noktasıdır, ancak etkisi bir çözüm üzerindedir. Bu da yalnız başına başarılı olmasını zorlaştırır. İkilik dizilerde değiştirme rasgele bir bit’in değiştirilmesiyle sağlanabilir. Çok düşük bir değiştirme olasılığı toplumda bazı özelliklerin kaybolmasına neden olabilir. Bu da en iyi sonuçların bulunmasına engeldir. Ancak yüksek bir değiştirme olasılığı da eldeki çözümleri bozarak sonuca ulaşmayı zorlaştırır. Gen takası ve değiştirmenin olasılıkları için kesin bir sayı yoktur. Değiştirme (mutasyon) olasılığı 0.01-0.001, gen takası (cross-over) olasılığı 0.5-1.0 aralığında tavsiye edilir.

Adım-4.
Eski kromozomlar çıkartılarak sabit büyüklükte bir toplum sağlanır.

Adım-5.
Tüm kromozomlar yeniden hesaplanarak yeni toplumunun başarısı bulunur.

Adım-6.
Genetik algoritma defalarca çalıştırılarak çok sayıda toplum oluşturulup hesaplanır.

Adım-7.
Toplumların hesaplanması sırasında en iyi bireyler saklandığı için o ana kadar bulunmuş en iyi çözüm çözümdür. Genetik algoritmanın yaptığı işleri temelini akış diyagramı olarak Şekil 9'de görebiliriz:

Basit bir genetik algoritma, L uzunluğundaki homojen bir çubuğun momentinin 0 (sıfır) olduğu noktayı bulmak için kurabiliriz.

L uzunluğuna bağlı olarak ara uzunluk x1 ve x2 0 ile 255 cm arasında işaretsiz bir tamsayı alınacaktır. F(x)=x1.m1-x2.m2 minimum değeri, aynı zamanda uygunluk fonksiyonudur. Dolayısıyla özgül kütleleri aynı olduğundan, doğrudan uzunluklara bağlı olacaktır. Yani uygunluk fonksiyonunu daha basit bir şekilde F(x)=x1-x2=0 olarak verebiliriz. Burada x2=L-x1 olduğundan F(x1)=2.x1-L=0 alınabilir. Örnek basit seçildiğinden sonucun matematik bilgisine göre 127.5 cm olacağı açıkça görülmektedir. 0 ile 255 arasındaki sayıları gösterebilmek için 8 bit uzunluğunda bir bilgiye ihtiyacımız vardır.

0................ 00000000
255............ 11111111

İlk olarak başlangıç topluluğu bu sayılar arasından rasgele olarak seçilebilir. Bunun için 8 birey oluşturulsun (N=8). Bunlar {0, 40, 80, 120, 160, 200, 220, 255} alınırsa:

0................ 00000000
40.............. 00101000
80.............. 01010000
120............ 01111000
160............ 10100000
200............ 11001000
220............ 11011100
255.............11111111

Değerleri başlangıç topluluğu olarak belirlenir. Bireylerin uygunluk değerleri, sayının ondalık karşılığının uygunluk fonksiyonuna verdiği cevapla bulunabilir. Uygunluk değeri sayının alabileceği değerler ile orantılı olursa, bunun için max uygunluk değeri olarak 255 ve minimum olarak ta 0 uygunluk değeri alınmalıdır. Eğer elde edilen uygunluk değeri 255 ten çıkarılırsa max uygunluğa 255 sayısının karşılık düştüğü görülebilir.
Örnek:

x=00000000 için F(x)=255-ABS(255–0)=0
x=00101000 için F(x)=255-ABS(255–80)=80 şeklinde belirlenebilir.

Bireylerin uygunluk değerlerinin rulete yansımasından kaç adet kopya oluşturulacağı veya hiç kopya alınmayacağı belirlenir. Yukarıdaki tabloya göre 80,120 ve 160 sayılarından 2 şer kopya alınacaktır. 0 ve 255 sayılarından hiç kopya alınmayacak ve diğer sayılardan 1 er kopya alınacaktır. Buna göre çaprazlama operatörü yardımıyla yeni bireyler üretmeden önce başlangıç topluluğu tekrar oluşturulmalıdır.

Yukarıdaki işlemlerde, bir nesilden diğer nesle kromozomlar aktarılırken, uygun kromozomların iyi özellikleri tekrar üreme adımında kullanılarak en iyi kromozomlar elde edilebilir. Elle yapılabilecek bu örnekte üç nesil sonra çözüm olabilecek bireylerin çözüm uzayını yeterince daraltarak birbirlerine daha çok benzeyecekleri görülecektir.

Genetik Algoritmaların Kullanılma Nedenleri

Öncelikle niye diğer yöntemlerin kullanılmadığı belirtilmelidir. Denklem en iyilemesinde (optimization);

1. Türev-İntegral hesabına (calculus) dayananlar
2. Numaralamaya (enumeration) dayananlar
3. Rastgele aramalar (random searches)

olmak üzere üç tip çözümden bahsedilir.
Genetik algoritmaların yeri Şekil 1.'de görülebilir.


Türev-İntegral hesaplamalarına dayanan hesaplama yöntemleri çok derinlemesine çalışılmıştır. Bu yöntemler fonksiyonun türevinin köklerinin fonksiyonun en küçük ve en büyük değer veren noktaları olmasından yararlanır. Gerçek problemler için sıfır veren noktaları bulmak da ayrı bir problemdir.
Diğer bir yöntem ise alınan bir noktadan sadece yukarı ilerleyerek en iyi sonucu bulmayı hedefler. Tepe tırmanma (hill climbing) denen bu yöntem fonksiyon grafiğinin tepelerini tırmanır. Ancak çok sayıda dönme noktası içeren bir fonksiyonda çok sayıda tepe oluşur. Hangi tepenin en iyi çözüm olduğunu bilenemez. Numaralama yöntemleri ise oldukça alışılagelmiştir. Sürekli olan gerçel sayı aralıkları belli sayıda parçaya ayrılarak parçalar denenir. Ancak problemler böyle çözmek için büyük olabilir. Bu yöntemin biraz daha geliştirilmiş şekli Dinamik Programlamayla (dynamic programming) oluşturulur. Parçalar arasından iyi görünenler seçilir. Bu parçalar parçalara ayrılarak işlem tekrarlanır. Bu yöntem de tepe tırmanma yöntemi gibi yanlış tepeleri araştırabilir. Dinamik Programlama tepelerin olmadığı aralıklarda başarılı ve hızlıdır.
En iyilemenin;

• Bir işin daha iyi yapılması
• En doğru şekilde yapılması

olmak üzere iki amacı vardır.
Günümüzde rasgele aramaların kullanımı artmaktadır. Bu tip aramalar en iyilemenin daha iyi yapma amacını sağlamakta daha başarılıdırlar. İnsanların bilgisayarlardan genel beklentisi mükemmellik olduğu için bu tip aramalar başarısız görünebilir. Genetik algoritmalar klasik yöntemlerin çok uzun zamanda yapacakları işlemleri kısa bir zamanda çok net olmasa da yeterli bir doğrulukla yapabilir.

Genetik Algoritmaların Farkları

1. Genetik algoritma parametrelerin kodlarıyla uğraşır. Parametreler kodlanabildiği sürece fark etmez.
2. Genetik algoritma bir tek yerden değil, bir grup çözüm içinden arama yapar.
3. Genetik algoritma ne yaptığı konusunda bilgi içermez, nasıl yaptığını bilir. Bu nedenle bir kör arama (blind search) metodudur.
4. Genetik algoritmalar olasılık kurallarına göre çalışır. Programın ne kadar iyi çalışacağı önceden kesin olarak belirlenemez. Ama olasılıkla hesaplanabilir.

Şema Teorisi (Schemata Theorem)

Genetik algoritmalarda oluşan başarılı bireyler incelenirse, bu bireyler arasındaki benzerlikler bulunabilir. Bu benzerliklerden yola çıkarak şemalar oluşturulabilir. İkilik dizi kodlaması için aşağıdaki yöntem önerilebilir.
0, 1 ve # (‘#’ o konumda 0 veya 1 olmasının önemsiz olduğunu gösterir).
Örnek olarak ikinci ve dördüncü bitleri 1, altıncı biti 0 olan çözümlerin başarılı olduğu bir toplumda şu şema oluşturulabilir:

#1#1#0

Tablo 1. Şema

Bu şemaya uygun aşağıdaki ikilik diziler yazılabilir:

010100, 010110, 011100, 011110, 110100, 110110, 111100, 111110.

Görüldüğü gibi şemaların katılması ikilik dizilerle gösterilen arama aralığını büyütmektedir. Arama aralığının büyümesinin sonucun bulunmasını zorlaştırması beklenir ancak durum böyle değildir. Seçilim ve yeniden kopyalama ile iyi özellikler daha çok bir araya gelerek daha iyi değerlere sahip şemalara uygun çözümler elde edilir.
Genetik algoritma kendi içinde sanal olarak şemaları oluşturur. Toplumun bireyleri incelenerek bu şemalar ortaya çıkarılabilir. Genetik algoritmalar şemaları oluşturmak için toplum üyelerinin kodları dışında bir bilgi tutmaz. Genetik algoritmaların bu özelliğine içsel paralellik (implicit parallelism) denir. Her nesilde, iyiyi belirleyen şemalardaki belirsiz yada önemsiz elemanlar azalır. Böylece genetik algoritmalar sonuca doğru belli kalıplar içinde ilerler.

GA’nın Performansını Etkileyen Nedenler

Kromozom sayısı
Kromozom sayısını arttırmak çalışma zamanını arttırırken azaltmak da kromozom çeşitliliğini yok eder.
Mutasyon Oranı
Kromozomlar birbirine benzemeye başladığında hala çözüm noktalarının uzağında bulunuyorsa mutasyon işlemi GA’nın sıkıştığı yerden kurtulmak için tek yoludur. Ancak yüksek bir değer vermek GA’yı kararlı bir noktaya ulaşmaktan alıkoyacaktır.
Kaç Noktalı Çaprazlama Yapılacağı
Normal olarak çaprazlama tek noktada gerçekleştirilmekle beraber yapılan araştırmalar bazı problemlerde çok noktalı çaprazlamanın çok yararlı olduğunu göstermiştir.
Çaprazlamanın sonucu elde edilen bireylerin nasıl değerlendirileceği
Elde edilen iki bireyin birden kullanılıp kullanılamayacağı bazen önemli olmaktadır.
Nesillerin birbirinden ayrık olup olmadığı
Normal olarak her nesil tümüyle bir önceki nesle bağlı olarak yaratılır. Bazı durumlarda yeni nesli eski nesille birlikte yeni neslin o ana kadar elde edilen bireyleri ile yaratmak yararlı olabilir.
Parametre kodlanmasının nasıl yapıldığı
Kodlananın nasıl yapıldığı en önemli noktalardan biridir. Örnek vermek gerekirse kimi zaman bir parametrenin doğrusal yada logaritmik kodlanması GA’nın performansında önemli bir farka yol açabilir.
Kodlama gösteriminin nasıl yapıldığı
Bu da nasıl olduğu yeterince açık olmamakla beraber GA’nın performansını etkileyen bir noktadır. İkilik düzen, kayan nokta aritmetiği ya da gray kodu ile gösterim en yaygın yöntemlerdir.
Başarı değerlendirmesinin nasıl yapıldığı
Akıllıca yazılmamış bir değerlendirme işlevi çalışma zamanını uzatabileceği gibi çözüme hiçbir zaman ulaşmamasına neden olabilir.

Genetik operatörlerin şema üzerine etkileri

1. Çoğalmanın etkisi

2. Çaprazlamanın etkisi

3. Mutasyonun etkisi

GA Nasıl Çalışıyor?

Gördüğümüz gibi GA'nın işleyişi çok basittir fakat bu kadar basit olan yöntemin, en zor problemleri nasıl çözdüğünün anlaşılması da o kadar zordur. Bu da GA’nın en karmaşık ve bilim adamlarının yıllardır çözmeye çalıştıkları en önemli sorulardan biridir.
GA’nın bu yönünü biraz açıklayalım; GA, çözüm(ler) bulmak için taranması gereken parametre uzayının çok büyük olduğu durumlarda bu arama işlemi, için en akılcı yöntemdir. Evrimin her sürecinde edinilen bilgi sonra ki nesillere aktarılarak taramanın daha uygun bölgelerde gezmesi sağlandığı gibi değişim işlemi yardımıyla yerel çözüm noktalarına sıkışıp kalma olasılığı da azaltılıyor. Ayrıca GA’nın paralel işlem yapılan bilgisayarlarda kullanılmaya elverişli yapısı da zaman alıcı problemlerin çözümü için çekici bir seçenek olmasını sağlamaktadır.

Örnek:

Fonksiyon Maksimizasyonu
Amacımız genetik algoritmanın bilgisayarda nasıl çalışacağını kağıt üzerinde açıklayıcı şekilde anlatmaktır.
Amaç
f(x)=x² , x Î[0,31] şeklinde verilen bir fonksiyonun, verilen aralıkta maksimizasyonu yapılması istenmektedir.

Adım 1:
İlk olarak x sayısının kodlanması işlemi yapılmalıdır. x’in 0 ve 1'lerden oluşan 2 tabanındaki gösterilimi kullanılacaktır. Dolayısıyla x, 5 bit uzunluğunda bir kodla (string) temsil edilecektir. Öyle ki 0: “00000” ve 31: “11111” olacaktır.

Adım 2:
Toplumun birey sayısı n:4 olarak seçilmiştir. Toplumu oluşturan dört birey, her biri 5 bit uzunluğunda birer kromozomla temsil edildiği için toplam 20 kere yazı tura atmak suretiyle belirlenmiştir. Elde edilen birey kromozomları aşağıdadır.

Birey 1: 01101, x = 13 , x² = 169
Birey 2: 11000, x = 24 , x² = 576
Birey 3: 01000, x = 8 , x² = 64
Birey 4: 10011, x = 19 , x² = 361

Adım 3:
Yukarıda belirlenen bireyler için f(x)=x², bireylerin uygunluk değerlerini verir. Dört bireyin toplam uygunluk değerleri “169+576+64+361=1170” dir. Dolayısıyla her bir bireyin rulet tekerleğinde kaplayacağı alan şu şekilde hesaplanır.

Birey 1: 169/1170=0.14 : %14
Birey 2: 576/1170=0.49 : %49
Birey 3: 64/1170=0.06 : %6
Birey 4: 361/1170=0.31 : %31

Bu değerler, rulet tekerleğinin her çevrilişinde hangi olasılıkla hangi bireyin seçileceğini belirtir, yani 0.14 olasılıkla 1 numaralı birey seçilecektir. Rulet tekerleği ve bireylerin tekerlek üzerindeki dağılımları Şekil 1.'de gösterilmiştir:

Adım 4:
Toplumda ki birey sayısının sabit kaldığı varsayıldığından dolayı, rulet tekerleği 4 kere çevrilerek çiftleşme havuzu oluşturulacaktır. Rulet tekerleği döndürülmüş ve şu sonuçlar elde edilmiştir.

Birey 1 : 1 kere
Birey 2 : 2 kere
Birey 3 : 0 kere
Birey 4 : 1 kere

Bunun sonucunda elde edilen çiftleşme havuzunda şu şekildedir;

Aday 1 : 01101 (Birey 1)
Aday 2 : 11000 (Birey 2)
Aday 3 : 11000 (Birey 2)
Aday 4 : 10011 (Birey 4)

Adım 5:
Çiftleşme havuzu belirlendikten sonra iki aşamalı çaprazlama uygulanır. İlk aşamada adaylar çiftleşmek üzere rasgele olarak eşlenirler. Her ikili grup için bir kere zar atılarak çaprazlaşmanın oluşacağı nokta belirlenir. rasgele eşleştirme yapılmış ve bunun sonucunca ( Aday 1, Aday 2) ve (Aday 3, Aday 4) ikili grupları oluşmuştur. Çaprazlaşma noktalarıca zar atılarak 1. Grup için k=4 ve 2. Grup içinde k=2 olarak belirlenmiştir. Bu aşamadan sonra çaprazlaşma gerçekleştirilmiş ve şu sonuçlar oluşmuştur; ( çaprazlaşma noktaları “/” ile belirtilmiştir.)

Çiftleşme grubu 1: (k=4)

Aday 1 : 0110/1 oluşan Birey 1 : 01100
Aday 2 : 1100/0 oluşan Birey 2 : 11001

Çiftleşme grubu 2 : (k=2)

Aday 3 : 11/000 oluşan Birey 3 : 11011
Aday 4 : 10/011 oluşan Birey 4 : 10000

Adım 6:
Son aşama olan mutasyon bitler düzeyinde uygulanır. Bu örnekte her bir bit için (toplam 20 bit var) mutasyon olma olasılığı 0.01 olarak seçilmiştir. Dolayısıyla her bir bit için ağırlıklı yazı/tura (mutasyon olasılığına göre) atılarak hangi bitlerin mutasyona uğrayacağı belirlenir. Bu işlem yapılmış ve sonuçta oluşan birey 3’ün 2 numaralı bitinde mutasyon olacağı ortaya çıkmıştır.

Oluşan Birey 3 : 11011

Mutasyon sonucu oluşan Birey 3 : 10011

Bu adımın tamamlanmasıyla bir sonraki kuşağı oluşturacak toplumun bireyleri
belirlenmiş olur. Yeni toplum şu şekildedir;

Birey 1 : 01100, x=12, x²=144
Birey 2 : 11001, x=25, x²=625
Birey 3 : 10011, x=19, x²=361
Birey 4 : 10000, x=16, x²=256

3 temel operatörden oluşan genetik algoritma her aşamada yeni oluşan kuşağa uygulanarak bir sonraki kuşak elde edilecektir. Yukarıdaki örnekte tek bir iterasyon yapılmış ve başlangıç toplumundan bir sonraki kuşak oluşturulmuştur ancak genetik algoritmanın çalışmasının tam olarak gözlenebilmesi için tek bir iterasyon yeterli değildir. Yukarıdaki işlemlerde her şey çok fazla rasgele gibi görünse de, uygunluk değeri yüksek olan bireylerin seçilme ve çiftleşme olasılıkları yüksek olduğu için kuşaklar ilerledikçe toplumu oluşturan bireylerin uygunluk değerlerinin ortalamasının da arttığı gözlenecektir. Bunun için ise tek bir iterasyon yeterli değildir.

GENETİK ALGORİTMALAR

Genetik Algoritma Kavramı

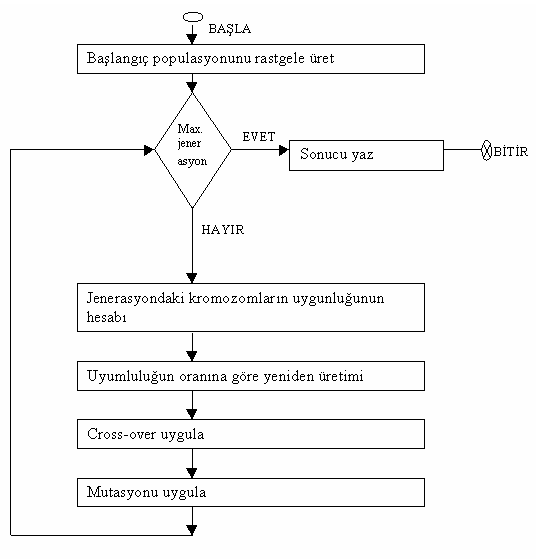
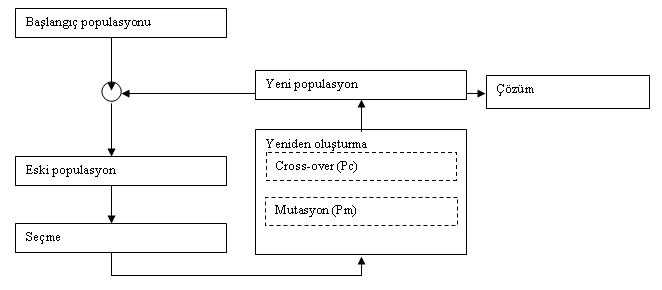
Genetik algoritmalar, karmaşık düzenli problemlerin çözümünü gerçekleştirmek amacıyla, kromozomların yeni diziler üretme esasını temel alan, sezgisel bir araştıma yöntemidir. Genetik algoritmalar, matematiksel fonksiyonların global optimizasyonunu hedeflerler. Genetik algoritmaları diğer araştırma yöntemlerinden ayıran özellik İse, bir çözüm seti ile başlandıktan sonra, geliştirme için biyolojik evrimi esas alan bir prosesin kullanılmasıdır. Bu prosesin sonunda da en iyi kromozoma ulaşma amaçlanmaktadır.Problemle ilgili parametreler, genler halinde bir araya gelerek kromozomu oluşturmakta; en iyi kromozoma ulaşma ise, genlerin kromozom içindeki dizilişini değiştirerek; yani, yeni nesiller yaratılarak gerçekleştirilmektedir. Genetik algoritmaların, problem çözümünde uygulanabilmeleri için, problemin çözüm uzayı olarak, her bir problemin mümkün çözümlerinden olan yapılardan (ya da organizmalardan) oluşan bir popülasyon ortaya konmaktadır. İlk neslin oluşması için, öncelikle belirli bir sayıda organizma seçildikten sonra, yeni bir neslin yaratılması için, mevcut nesilden seçilen aiie'lere bazı genetik oparatörler uygulanır. Burada "iyi çocuklar iyi aileden doğar" fikrine uygun olarak, mevcut nesil içinde yüksek uygunluk değerine sahip organizmaların aile olarak seçilme şansları da doğal olarak yüksektir.

Genetik algoritmaların özellikleri

Çeşitli problemlerin çözümünde kullanılan genetik algoritmlar, aşağıdaki özellikleri taşırlar.
a) Uygun çözümler için bir veya daha fazla "popülasyon" mümkündür.
b) Önceden bilinen çoklu çözümlerin özelliklerini bir araya getirerek, yeni uygun çözümler üreten bir mekanizmaya sahiptir.
c) Önceden bilinen bir çözümün düzenini rast gele (tesadüfi) bir şekilde değiştirerek, yeni uygun bir çözüm üreten bir mekanizmaya sahiptir.
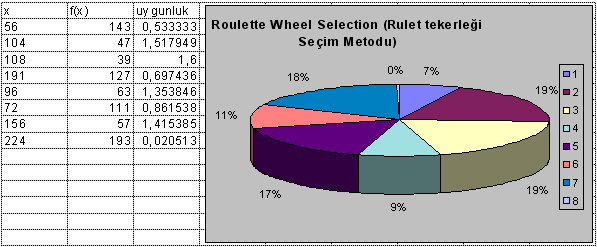
d) Popülasyon içinden, öncelik vererek, ayrı çözümleri seçen bir mekanizmaya sahiptir.
e) Popülasyon içinden bazı çözümleri dışarı çıkaran bir mekanizmaya sahiptir.

Genetik algoritmaların sahip olması gereken koşullar

Genetik algoritmaların etkin bir şekilde kullanılabilmeleri için, aşağıdaki koşulların sağlanması gerekmektedir.
a) Araştırma uzayı parametreleri, ikili (0-1) sistemde veya alfabetik bir şekilde kodlanarak belirli bir uzunlukta kromozom-gen düzeni oluşturulmalıdır.
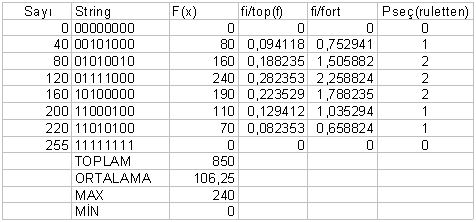
b) Uygun çözüm sayısını azaltmak için problemin amacı doğrultusunda bir uygunluk fonksiyonu kullanılmalıdır.
c) Paralel ve global araştırmaya imkân sağlanması açısından, araştırma uzayı içindeki her nokta taranmalıdır.
d) Bir araştırma uzayından diğerine bir gelişme sağlanabilmesi için, olasılıklı geçiş (değişim) kuralı kullanılmalıdır.

Genetik Operatörler

Genetik algoritmalardaki kromozom yapıların kopyalanması işleminde üç temel operatör kullanılmaktadır. 

Yeniden üretim (reproduction)
Her bireyi, bir nesilden diğerine aynen kopyalama işlemidir. Uygunluk derecesi yüksek olan kromozomlar üşütün nitelikli çocuk üretiminde kullanılmak üzere bu yöntemle çoğaltılırlar.

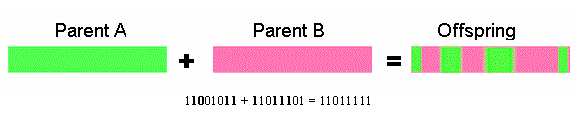
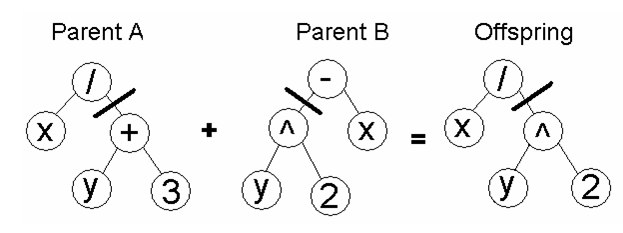
Çapraz değişim (crossover)
İki veya daha fazla kromozomdan (aile'den), yeni bir kromozom (çocuk) meydana getirme işlemidir. Burada da amaç, daha iyi niteliklere sahip çocuklara ulaşmaktır.

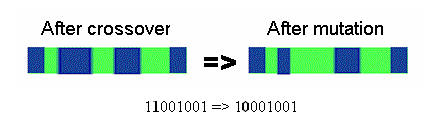
Dahili değişim (mutation)
Kromozom yapısı içinde değişikler yapma işlemidir. Mustasyon işlemi ile yeni uygun çözümler elde edilmeye çalışılır.

Nümerik Kodlama

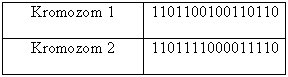
Problemdeki parametreleri temsil eden, kromozom yapısı içindeki genlerin dizilişinin gösterimi, daha çok ikili sistem (0-1 sistemi) veya diğer rakamların da kullanılmasıyla gerçekleştirilmektedir. Rakamların ikili sistem dışında kullanımında, problemin paremetreleri gereği, sıralı veya sırasız rakamların birer defa kullanımının yanısıra, aynı rakamların birden çok kullanımına da rastlanmaktadır.

Çapraz değişim uygulamaları

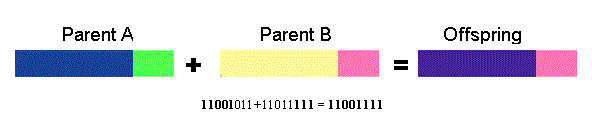
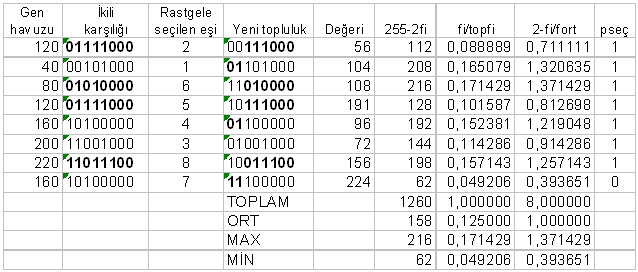
Çapraz değişim ile ilgili olarak rastlanılan ilk uygulama şeklinde, önce kromozom yapı üzerinde rast gele bir ayrım noktası belirlenmektedir. Kromozonlar, çapraz değişim işleminde bu ayrım noktası öncesindeki gen yapısını aynen korurlarken, ayrım noktası sonrasındaki gen yapısını ise karşılıklı olarak değiştirmektedirler. Takip eden örnekte de görüleceği gibi, ayrım sonrası genleri (1100) ve (1010) karşılıklı olarak yer değiştirmiş.

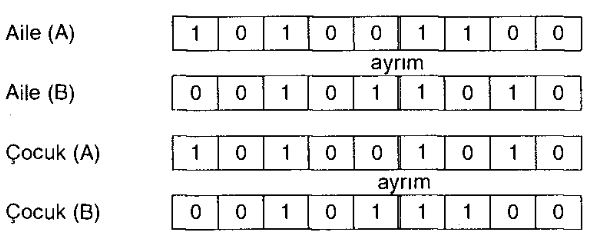
Bazı uygulamalarda ise, iki ayrım noktası kullanılmaktadır. Ayrım noktalarının belirlenmesi ve karşılıklı değiştirilecek parçaların belirlenme işlemleri yine rast gele olmaktadır. Takip eden örnekte, iki ayrım noktası arasındaki (001) ve (011) genleri karşılıklı yer değiştirmiştir

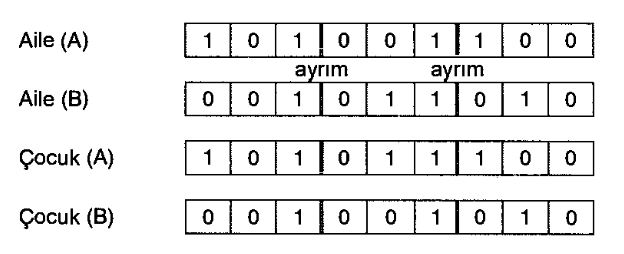
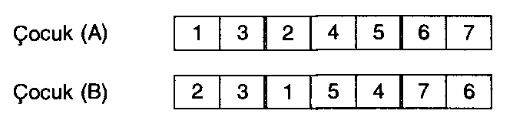
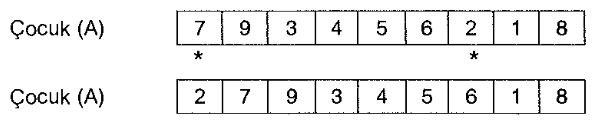
Bazı çapraz değişim uygulamalarında, ailedeki kalıtsal özelliklerin çocuğa taşındığı durumlara ratslanmaktadır. Tahip eden örnekte ile işaretlenen kalıtsal özelliklerin, çocuk (A)'ya ne şekilde taşındığı gösterilrnektedir.

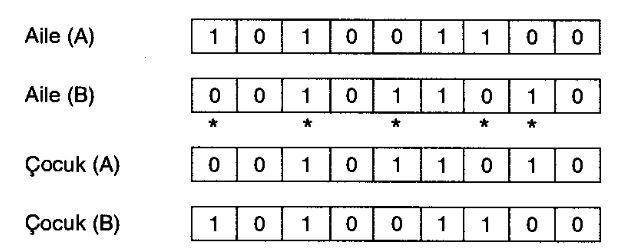
Bazı uygulamalarda, çapraz değişimin hemen arkasında bir onarma işlemine ihtiyaç olmaktadır. Bunu, takip eden örnekte görebiliriz.

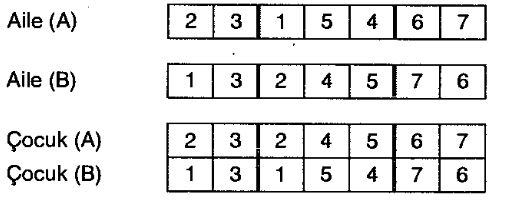
iki ayrım arasındaki genler karşılıklı değiştirildiğinde, elde edilen sonucun uygun olmadığı açıkça gözükmektedir. Takip eden örnekteki onarma
işleminde, birinci sıradaki genler karşılıklı değiştirilerek uygunluk sağlanmıştır.

Görüldüğü gibi çapraz değişimle ilgili çok çeşitli uygulamalar söz konusudur. Burada önemli olan uygunluk derecesi yüksek olan aileleri bir araya getirerek, uygunluk derecesi daha yüksek çocuklar elde etmeye çalışmaktır. Bu arada, uygunsuz olan sonuçların ortaya çıkması durumunda, onarım işlemi uygulanmalıdır.

Dahili değişim (mutasyon) uygulamaları

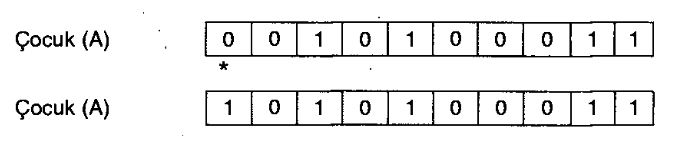
Kromozom yapısı üzerindeki dahili değişim, genellikle rast gele bir şekilde belirlenen bir gen'in değiştirilmesiyle gerçekleştirilmektedir. Yani, 1 ise O'la veya 0 ise 1'le değiştirilmektedir.
İkili sistem yerine, problemin paremetreleri gereği, sıralı veya sırasız rakamların birer defa ya da aynı rakamların birden çok kullanımının söz konusu olduğu durumlarda, rast gele belirlenmiş herhangi bir gene ait rakam, yine rast gele belirlenmiş diğer rakamla yer değiştirmektedir. Takip eden örnekte ise, kromozomda ile işaretlenmiş gen rast gele bir şekilde belirlenerek değiştirilmiş, böylelikle mutasyon işlemi tamamlanrnıştır.

Bazen de kromozom üzerinde iki gen rast gele seçilerek, karşılıklı olarak yer değiştirmeleri sağlanır. Takip eden örnekte, 3. ve 8. sıradaki genler rast gele seçilerek, yerleri değiştirilmiştir.

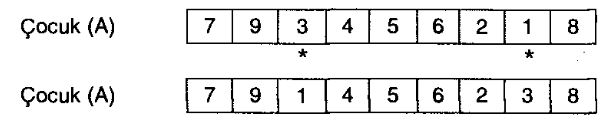
Bazı uygulamalarda ise, rast gele seçilen gen bulunduğu sıradan alınarak, yine rast gele olarak belirlenen başka bir sıradan yapıya dahil edilir.
Takip eden örnekte de gösterildiği gibi, 7. Sırada bulunan gen (2), sırasından çıkarılarak 1. Sıradan tekrar yapıya dahil edilmiştir.

Alfabetik Kodlama

Prablemdeki parametreleri temsil eden, kromozom yapısı içindeki genlerin dizilişinin gösterimi, alfabetik sembollerin kullanılmasıyla da gerçekleştirilmektedir. Bu gösterim şeklinde, rakamlarla gösterim şeklinde de olduğu gibi, sıralı veya sırasız harflerin birer defa ya da birden çok kullanımına rastlanmaktadır.
Çapraz değişim ile ilgili uygulamalar incelendiğinde, en çok rastlanı- lanların, takip eden dört örnekteki gibi olduğu görülecektir.
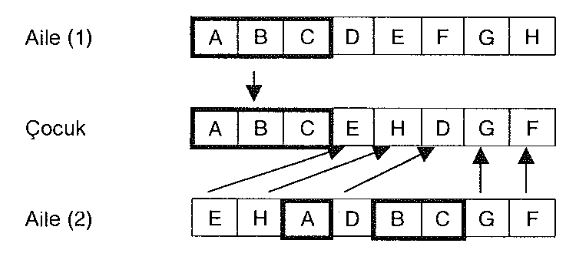
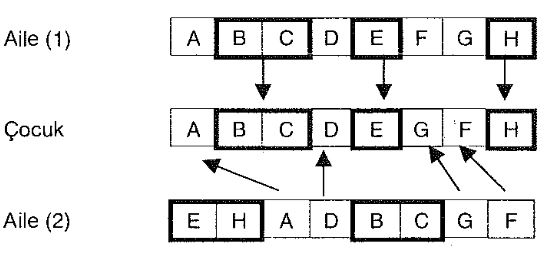
Takip eden örnekte, tek ayrım noktasının söz konusu olması durumundaki çapraz değişim gösterilmektedir. Görüldüğü gibi, Aile (1)'den alman (ABC) genleri, Çocuk'ta aynı sırada ve aynı pozisyonda yer alırken; (EHDGH) genleri ise, Aile (2)'den alınarak yine aynı sıra ile sıralanmaktadır.

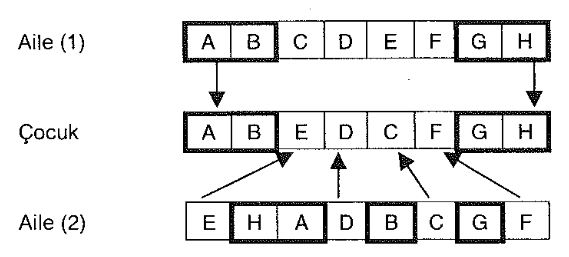
iki ayrım noktasının olması durumunda, takip eden örnekte de görüldüğü gibi, Aile (1)'den alınan (AB) ve (GH) genleri aynı pozisyonda Çocukta da yer alırken; Aile (2)'den alınan diğer genler (EDCF) de aynı sıra içersinde Çocuk'ta da yer almaktadır.

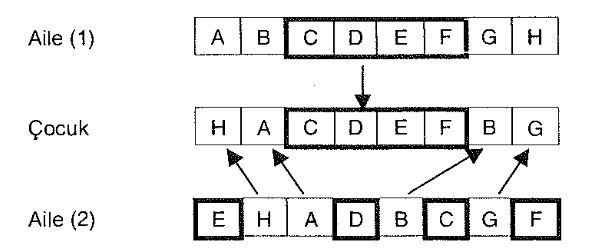
Yine iki ayrım noktasının olması durumunda, ancak bu defa Aile (1)'den alınan (CDEF) genleri aynı pozisyonda olmak üzere Çocuk'ta yer alırken; Aile (2)'den alınan diğer genler de aynı sırada Çocuk'ta yer almaktadır.

Takip eden örnekte ise, Aile (1)'den rast gele seçilen işaretli genler, Çocuk'ta kalıtımsal olarak ayın pozisyonlarda yer alırken; Aile (2)’den alınan diğer genler (ADGF) de, kalan pozisyonları yine aynı sırada doldurmuştur.

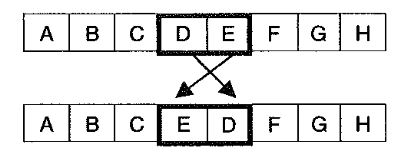
Dahili değişim (mutasyon) uygulamaları

Dahili değişim (mutasyon) ile ilgili uygulamalar incelendiğinde, en çok rastlanıîanların, genellikle takip eden dört örnekte gösterildiği gibi olduğu görülecektir. Takip eden ilk örnekte, rast gele seçilen iki komşu genin, karşılıklı olarak değiştirilmesiyle mutasyon gerçekleştirilmektedir.

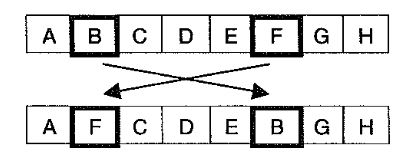
Takip eden diğer örnekte de gösterildiği gibi rast gele seçilen iki gen, karşılıklı olarak da değiştirilebilmektedir.

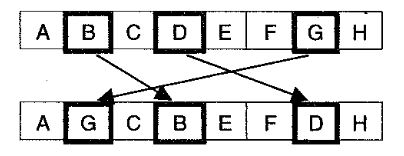
ilk iki örneğin özel bir durumu olarak nitelendirebileceğimiz üçüncü örnekte, üç gen rast gele seçilerek, yine rast gele sırada yeniden sıralanmaktadır.

Takip eden bu son örnekte ise, rast gele geçilen bir gen, yine rast gele bir şekilde seçilen poziyonda araya sokulmakta; değer genler ise ok istikametinde kaydırılmaktadır.

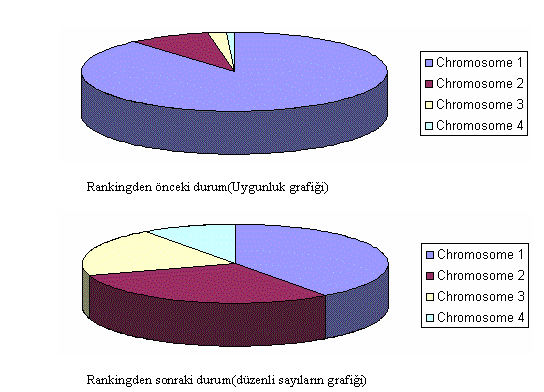
Değerlendirme

Yeniden üretim (reproduction), çapraz değişim (crossover) ve dahili değişim ya da mutasyon (mutitation) aşamalarının her tamamlanışında,
sonuçların öncekilerle karşılaştırılması gerekmektedir. Buradaki amaç en iyi kromozomu elde etmek; başka bir ifade ile, en iyi çözüme ulaşmaktır. Bu nedenle, her çevrimde elde edilen yeni kromozomların uygunluk dereceleri belirlenerek, sıralamaya dahil edilirler. En iyiler "Aile" görevi ile yeni nesil üretimine devam ederek, daha iyi nitelikli "çocuk" elde edilmesine çalışırlar. Bu süreç, amaç gerçekleşinceye kadar devam eder.

Genetik Algoritmaların Kullanım Alanları
Genetik algoritmalar, özellikle 1985 yılından sonra, gittikçe artan bir ilgiyle geniş bir kullanım alanına sahip olmaya başlamıştır. Bu kısımda özellikle son yıllarda gerçekleştirilen genetik algoritma uygulamaları tanıtılmaya çalışılmıştır.

GA'lann doğrusal olmayan tam sayılı programlamada kullanımı
Bu konuda yapılan çalışmalara, Yokota ve arkadaşlarının, 1995 yılında yayınlanan iki makalesinde rastlan maktadır. Bu çalışmalarda, optimum sistem güvenilirliği ile ilgili doğrusal olmayan tam sayılı programlama problemi, aralık katsayıları kullanılmadan; doğrudan, amaç fonksiyonunun doğrusal olmama durumu da korunarak, genetik algoritmaların kullanılmasıyla çözülmüştür.

GA'ların Hücresel imalat problemlerinde kullanımı

Bu konuda yapılan çalışmalardan bir tanesinde (1996), Joines ve arkadaşları (Culbreth & King), hücresel imalat tasarımı probleminin çözümünde, tam sayılı programlama ve genetik algoritmaları beraberce kullanmışlardı r(JolneS). Hwang ve arkadaşı (Sun) ise yine 1996 yılında yayınlanan makalede, hücre oluşumu probleminin çözümü için, genetik algoritma tabanlı, iki fazlı sezgisel bir çözüm önermişlerdir.

GA'lann motaj hattı dengeleme problemlerinde kullanımı
Bu konuda, Gen ve Tsujimura ile arkadaşlarının Gerçekleştirdikleri çalışmalarla ilgili olarak 1995 yılında yayınlanan makalelerinde; her bir iş istasyonundaki toplam işlem zamanlarını minimize etmeyi hedefleyen genetik algoritma amaç fonksiyonu ile bulanık küme mantığı beraberce kullanılarak, montaj hattı dengeleme problemlerinin çözümü gerçekleşti rilmiştir.

GA'lann yerleşim (layout) problemlerinde kullanımı
Yerleşim konusunda çalışma yapan Cheng ve arkadaşlarının (Gen & Tosowa) 1995 yılında yayınlanan makalelerinde, makinaların dairesel olarak yerleştirildiği ve malzeme hareketinin tek bir yöne doğru gerçekleştirildiği durum ile ilgili problemin, genetik algoritmalar ile sezgisel bir yöntem kullanarak çözülebileceğini göstermişlerdir(Cheng). Yerleşim konusundaki bir diğer çalışma ise Gen ve arkadaşları tarafından 1995 yılındaki makalelerinde sunulmuştur. Bu makalede, makinalar arası toplam taşıma maliyetlerinin minimize edilmesinin hedeflendiği, çok hatlı makine yerleşim problemi, bulanık küme mantığı ile genetik algoritmalar kullanılarak çözülmüştür.

GA'lann atama problemlerinde kullanımı
Bu konuda araştırma yapan Chu & Beasly, 1996 yılında yayınlanan makalelerinde, minimum maliyetli atamanın hedeflendiği problem için genetik algoritmaların kullanıldığı bir çözüm önermişlerdir(Chu). Bu konudaki diğer bir çalışma da, Tate ve Smith tarafından 1994 yılında yayınlanan makalelerinde sunulmuştur. Bu çalışmada, kuadratik atama probleminin çözümü genetik algoritmalar ile gerçekleştirilmiştir(Tate). Yine bu konudaki başka bir çalışmada, Zhao ve arkadaşları 1995 yılında yayınlanan makalelerinde, iş istasyonu atama problemi (ve robot seçimi) için genetik algoritmaları kuilanmışlardır.

GAİarın sıralama problemlerinde kullanımı
Bu konuda yapılan çalışmalarda, Reeves 1994 yılında yayınlanan makalesinde, genetik algoritmaları n-adet iş ve m-adet makine'nin söz konusu olduğu akış atölyesi sıralama probleminin özümünde kullanılmasını tanıtmıştır. Bir başka çalışmada ise, Yip-Hoi ve Dutta, 1996 yılında yayınlanan makalede, bir tezgahın iki farklı talaş kaldırma işlemi yapabilmesi durumunda, proses planlamadaki sıralama probleminin çözümü için genetik algoritmaları kullanmışlardır. Kim ve arkadaşlarının (Hyun & Kim), karışık model montaj hatlarındaki sıralama problemi için, 1996 yılında yayınlanan makalelerinde, önerdikleri genetik algoritmalar yaklaşımı, büyük çaplı sıralama problemlerinin çözümünde, makul bir hesaplama süresi içinde optimuma yakın sonuçlar verrnektedir. Yine aynı konuda gerçekleştirilen bir diğer çalışmada da, Leu ve arkadaşları (Matheson & Rees) tarafından gerçekleştirilmiştir. Bu araştırma ile ilgili olarak 1996 yılında yayınlanan makalede, kullanılan yapay zeka tabanlı genetik algoritma yöntemi ile iyi bir sonuç elde edildiği vurgulanmaktadır. Bir başka çalışmada ise Rubin ve Ragatz, tek makina-n-adet iş, sıralama probleminin çözümü için 1994 yılında yayınlanan makalelerinde, önerdikleri genetik algoritmalar yaklaşımının, dai- sınır algoritması kadar iyi sonuç vermese de, kullanımını tavsiye etmektedirler. Bir diğer çalışmada ise Usher ve Bovvden, 1996 yılında yayınlanan makalelerinde, bilgisayarla bütünleşik proses planlamada operasyon sıralama pobieminin çözümü için genetik algoritmaların kullanılması ile iyi bir performans sağladıklarını vurgulamaktadırlar.

GA’ların çizelgeleme problemlerinde kullanımı
Bu konuda yapılan çalışmalarda, Chen ve arkadaşlarının (Nepalli & Aljaber) 1996 yılında yayınlanan makalelerinde, akış atölyesi çizelgeleme probleminin çözümü için genetik algoritmalar esaslı sezgisel bir yöntem önerilmiştir. Yine bu makaledeki uygulamada, genitik algoritmaların çizelgeleme problemlerinde kullanımının (daha da geliştirilebilir) iyi sonuçlar verdiği vurgulanmaktadır. Bir başka çalışmada ise, Murata ve arkadaşları (ishibuchi & Tanaka) 1996 yılında yayınlanan bir makalelerinde, akış atölyesi çizelgeleme probleminin çözümü için iki hibrit genetik algoritma önerilmiştir. Aynı ekibin bir başka makalesinde ise, bu defa çok- amaçlı genetik algoritmaları, akış atölyesi çizelgeleme probleminin çözümü için önermektedirler. Çok-amaçlı genetik algoritmaların; tek-amaçlı genetik algoritmalardan ve Schaffer'in önerdiği VEGA’dan (Vector Evaluated Genetic Algorithm) daha iyi sonuç verdiği vurgulanmaktadır. Çizelgeleme konusunda yapılan bir başka çalışmada ise, Sakawa ve arkadaşları (Kato & Mori) 1996 yılında yayınlanan makalelerinde, uygulanan genetik algoritmaların, çözümü istenen probleme uygun olması gerektiğini belirterek; esnekliğin göz önüne alındığı, uygun bir genetik algoritmayı, bir işleme merkezindeki çizelgeleme problemi için önermişlerdir. Croce ve arkadaşlarının (Tadei & Volta) yaptığı çalışma ise, sipariş atölyesi çizelgeleme probleminin çözümü ile ilgilidir. 1994 yılında yayınlanan makalelerinde önerdikleri genetik algoritmanın, gerek önceki GA uygulamaları gerekse de diğer bazı sezgisel yöntemlere üstünlüğü vurgulanmaktadır. Bir diğer araştırmada, Sikora tarafından yapılan çalışma 1996 yılında yayınlanan makalesinde tanıtılmıştır. Bu çalışmada, parti hacmi ve sıralama kararlarını beraberce içeren bir çizelgeleme problemi üzerinde durulmuştur. Önerilen genetik algoritma ile bu zor problemin çözümü gerçekleştiril-
miştir.

GA'lann diğer kullanım alanları
Bu makalede tanıtma imkanı bulunamayan daha bir çok konuda da, genetik algoritmaların kullanımına rastlanmaktadır. Bunlar, bilgisayarla bütünleşik tasarım, gezgin-satıcı problemi, tamir-bakım politikası, tahmin yöntemleri, dağıtım ve transport poblemleri, Araç-rota problemleri, Paketleme problemleri ve vb. gibi konulardır.

Genetik Çeşitliliği Göz Ardı Eden Algoritmalar!

Yapılan araştırmalara göre algoritmaların, insanlar arasındaki çeşitliliği görmezden gelen veri tabanlarına dayalı bir nitelik taşıdığı saptandı. İlgili araştırma bağlamında, Google aramalarında karşılaştığı sonuçların ağırlıklı olarak 'beyaz' renk yönünde olması üzerine 'World White Web Project' adlı siteyi kuran grafik tasarımcısı Johanna Burai, konuyla ilgili farkındalığın giderek arttığını belirtiyor. Söz konusu farkındalığın en iyi örneğini ise algoritmalarda adaletin sağlanması amacıyla kurulan Algorithmic Justice League (AJL) oluşturuyor.

Google ise yöneltilen eleştiriler bağlamında görsel arama sonuçlarının kendi değerlerinden tamamen bağımsız olduğunu belirterek, ilgili sonuçların internet içeriğinde hangi görsellerin yaygın kullanıldığı ve bunların nasıl tanımlandıkları ile ilgili bir sunum olduğunu belirtiyor.

Öte yandan Massachusetts Institute of Technology'de (MIT) doktora öğrencisi olan Joy Buolamwini, yüz tanıma programını kullanan yapay zekanın ten rengi nedeniyle kendisini tanımadığını, bu noktada beyaz maske kullanmak zorunda kaldığını belirtiyor. Sınırları genişleten Buolamwini'ye göre obeziteli, aşırı kilolu bireylerde söz konusu algoritmaların nasıl çalıştığı da ayrı bir araştırma konusu. Ayrıca cilt kanserini tanıyan bir algoritmanın siyah tene sahip bireylerde çalışıp çalışmadığı da yine araştırmacılar tarafından AJL'ye danışılmış.

Algoritmalardaki bir başka sorunun teknoloji endüstrisinde çalışanlar içindeki etnik çeşitlilik eksikliği olduğunu belirten Buolamwini, dev teknoloji şirketlerine ait her yıl yayınlanan çeşitlilik raporlarının da bu tezi desteklediğini öne sürüyor.

Dev Teknoloji Şirketlerinin Yayınladığı Çeşitlilik Raporları!

• Ocak 2016'da paylaşılan Google'ın son raporuna göre şirketin teknik departmanında çalışanların sadece yüzde 19'unun kadın olduğu, yüzde 1'inin de siyahlardan oluştuğu belirtiliyor.
• Eylül 2016'da Microsoft tarafından yayınlanan rapora göre çalışanların yüzde 17.5'inin kadın ve yüzde 2.7'sinin siyah veya Afrikalı ve Amerikalı olduğu belirtiliyor.
• Haziran 2016'da Facebook'un yayınladığı rapora göre ise departmanın yüzde 17'sinin kadın ve yüzde 1'inin de siyahlardan oluştuğu belirtiliyor.

Söz konusu genetik algoritmalara yönelik yapılan araştırmalar, suça eğilimde siyah tene sahip bireylerin beyaz tene sahip bireylere oranla daha yüksek bir orana sahip olduğunu da gösteriyor. Araştırmacılara göre algoritmalardaki taraflılığın kesin bir doğru olarak algılanmaması için çözüm odaklı bazı kriterler gerekli.

Önerilen Çözüm Odaklı Kriterler!

• Algoritmaları eğitmek, geliştirmek adına çeşitli veri tabanlarının üretilmesi.
• Program ve yazılım satıcıları arasında ilgili alışkanlığın yaygın hale getirilmesi.
• Karar verme sürecindeki ön yargılara dair, kullanıcıları bilgilendirecek nitelikte algoritmaların kurulması.

Kaynak: BBC Bilim / Science (15 Nisan 2017)