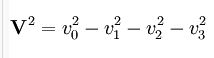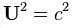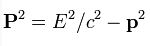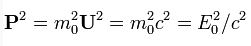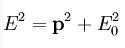Ziyaretçi
ÖZEL GÖRELİLİK KURAMI
Tarihsel gelişim
Sponsorlu Bağlantılar
Newton’a göre, herhangi iki eylemsiz referans sistemi birbirlerine göre doğrusal, düzgün ve dönmeksizin (doğrultusu değişmeyen ve sabit hızla) hareket eder ve iki sistemdeki saatler (yeryüzünde iki farklı saat diliminde bulunan saatler gibi aralarında sabit bir fark bulunsa da aynı hızla işler. Bu nedenle, herhangi iki olgu, bu eylemsiz sistemlerden birindeki gözlemci tarafından eşzamanlı olarak gözlenirse, tüm öbür gözlemcilere de eşzamanlı görünecektir. Zamanın ve zaman belirlemelerinin bu evrenselliği, genellikle zamanın mutlak karakteri olarak adlandırılmıştır.
Fiziksel evrenin yapı taşlarının parçacıklar olduğu ve boş uzayda birbirleriyle etkileşen parçacık sistemlerinin Newton’un öngördüğü ilkelere uyduğu düşünüldüğü sürece, klasik fizikteki uzay ve zaman kavramlarının geçerliğinden kuşkulanmak için bir neden bulunmamaktaydı. Ama 19. yüzyılda elektriksel ve magnetik olayları inceleyen Hans Christian Orsted ve Michael Faraday’ın buluşları ile James Clerk Maxwell’in kuramsal çalışmaları, bu doğa görüşünün yeniden sorgulanmasını zorunlu kıldı.
Elektrik yüklü cisimler ve mıknatıslar, aralarında çok büyük uzaklıklar bulunduğunda birbirlerini neredeyse hiç etkilemezler; ama görece yakın olduklarında uzayda saniyede yaklaşık 300.000 km hızla yayılan bir elektromagnetik alan aracılığıyla etkileşirler. İçinde bildiğimiz hiçbir madde bulunmayan bölgelerde elektrik ve magnetik alanları neyin taşıdığı, elektromagnetik alan kuramını öne süren Maxwell ile laboratuvarda bu dalgaları elde eden Heinrich Hertz’in başlıca sorunu olmuştu. O güne değin, sonlu hızla yayıldığı bilinen alan ve dalgalar, su dalgaları gibi yüzey dalgaları ile deprem şokları gibi düşük frekanslı dalgalar ve ses duyusu olarak algılanan dalgalardı. Maxwell, elektromagnetik dalgaların uzaydaki gizemli taşıyıcısına esir (eter) adını verdi. Elektromagnetik dalgaların bilinen özelliklerini taşıdığı düşünülen esir kavramı, bu taşıyıcının varlığının deneysel olarak saptanması sorununu ortaya çıkardı.
1887’de iki ABD’li fizikçi, Albert Abraham Michelson ile Edward Willams Morley, yeryüzü üzerinde esirin hızını ölçmek için bir deney tasarladılar. Yer’in evrenin ekseni olmadığı varsayımı geçerli ise, farklı doğrultularda yol alan ışık ışınlarının (Yer’e ve laboratuvar aygıtlarına göre) gözlenen hızlan arasında, Yer’in esire göre hareketi nedeniyle küçük farkların ortaya çıkması gerekiyordu. Eğer bir ışık demetinin ayna yardımıyla ileri ve geri yönlerde yol alması sağlanırsa, belli bir konum için toplam gidiş geliş süresi ölçülerek demetin hızı bulunabilir. Hızın mutlak değeriyle değil de iki ayrı yoldaki hızların farklarıyla ilgileniliyorsa, birbirine dikey iki yoldaki gidiş geliş süreleri karşılaştırabilir. Michelson ve Morley, saat kullanmaktan kaçınmak için, dikey yönlerde yol alan ışık demetlerinin birbirleri ile optik girişim yapmalarını sağlayarak bu iki demetin gidiş geliş sürelerini dalga-boylannın sayısı cinsinden karşılaştırdılar. Bu çok duyarlıklı deney, sürekli geliştirilen tekniklerle birçok kez yinelendi. Elde edilen birbiriyle uyumlu sonuçlar, ışık hızının, yılın hangi gün ve saatinde ölçüldüğüne ya da laboratuvarın konumuna bakmaksızın her doğrultuda aynı olduğunu gösterdi.
Özel görelilik kuramı,bu deneysel bulgudan kaynaklandı: Yeryüzündeki gözlemci, Yer’in esir içindeki hareketini saptayamadı- ğına göre, hareket durumu ne olursa olsun herhangi bir gözlemci için ışığın her doğrultudaki hızı aynı olmalıydı.
Uzayın ve zamanın göreliliği
İrlandalI fizikçi George Francis FitzGerald ve HollandalI fizikçi Hendrik Antoon Lorentz, Michelson-Morley deneyinin sonuçlarına yeni bir yorum getirdiler: Esir içinde hareket eden bir cismin, harekete dikey doğrultulardaki boyutları değişmeden kalmak üzere, hareket doğrultusundaki boyu kısalırsa, deney sonuçları ile esir kavramı uzlaştırıla- bilirdi. Cismin esire göre hızı v ve ışığın hızı c ile gösterilirse, kısalmayı veren oran
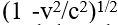 olur. Alışılmış hızlar, ışık hızından çok küçük olduğundan
olur. Alışılmış hızlar, ışık hızından çok küçük olduğundan 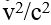 pratikte sıfırdır; kısalma gözlenemez. Ama v hızı, ışık hızına yaklaştığında bu oran önem kazanır. Örneğin, ışık hızının yaklaşık yüzde 87’si kadar bir hızla hareket eden bir Cismin boyu, durgun boyunun yansına inmiş görünür.
pratikte sıfırdır; kısalma gözlenemez. Ama v hızı, ışık hızına yaklaştığında bu oran önem kazanır. Örneğin, ışık hızının yaklaşık yüzde 87’si kadar bir hızla hareket eden bir Cismin boyu, durgun boyunun yansına inmiş görünür.Lorentz aynca, esirde hareket eden saatlerin, durgun saatlere göre, gene
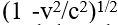 oranında yavaşladıklarının gözleneceğini de öne sürmüştür. Böylece esir içinde hareket eden tüm cetveller ve saatler, yapıldıkları malzemeden ve tasanmlarından bağımsız olarak sistematik değişikliklere uğrarlar. Bu nedenle kuramsal çözümlemeler yapılırken “görünür” ve “gerçek” uzay ve zaman ölçümleri arasında ayrım gözetilmelidir. Aynca “gerçek” zaman ve boyutların herhangi bir deneysel işlemle bulunamayacağı da göz önünde tutulmalıdır.
oranında yavaşladıklarının gözleneceğini de öne sürmüştür. Böylece esir içinde hareket eden tüm cetveller ve saatler, yapıldıkları malzemeden ve tasanmlarından bağımsız olarak sistematik değişikliklere uğrarlar. Bu nedenle kuramsal çözümlemeler yapılırken “görünür” ve “gerçek” uzay ve zaman ölçümleri arasında ayrım gözetilmelidir. Aynca “gerçek” zaman ve boyutların herhangi bir deneysel işlemle bulunamayacağı da göz önünde tutulmalıdır.Kavramsal açıdan tatmin edici olmayan bu durum 1905’te Albert Einstein tarafından çözüme kavuşturuldu. Einstein farklı hareketler yapan gözlemciler arasındaki bütün karşılaştırmalarda anahtar kavramın evrensel (mutlak) eşzamanlılık kavramı olduğunu gördü. Bu, bir gözlemciye eşzamanlı görünen iki olgunun başka bütün gözlemciler için de eşzamanlı olarak algılanacağı anlamına gelir. Çok uzaktaki olguların anında gözlenebileceği kabul edilirse, bu, çok yalın bir önermedir. Ama gerçekte ışıktan ya da başka elektromagnetik ışınımlardan daha hızlı bir haber ulaştırma yöntemi bilinmemektedir. Yeryüzündeki bir gözlemcinin göğün farklı bölgelerindeki iki süpernovayı gözlediğini düşünelim. Yalnızca gökte görülmeleri sonucunda bu iki süpernovamn eşzamanlı patlayıp patlamadıkları söylenemez; gözlemciye göre uzaklıklarının da bilinmesi gerekir. Gökcisimleri binlerce ışık yılı uzaklıkta bulunabileceklerinden, süper- novalardan birinin öbüründen çok önce patlamış olması ve yola çıkardığı ışınların binlerce yıl geçtikten sonra öbürünün ışığı ile eşzamanlı olarak gözlemciye ulaşması çok olasıdır. Dolayısıyla bir gözlemci için iki olay eşzamanlı gözükürken, farklı hızlarda hareket eden gözlemciler için bu iki olay eşzamanlı gözükmeyebilir. Demek ki eşzamanlılığın göreli olduğu göz önünde tutulmalıdır.
Bu kuramsal çıkarsama, FitzGerald ve Lorentz’in bulgularının yeniden yorumlanmasına yol açtı. Birbirlerine göre hareketli olan eylemsiz referans sistemlerindeki gözlemcilerin, zaman aralıkları ve uzaklıklar için yaptıkları belirlemeler, sistematik biçimde uyuşmazlık içinde olacaktır. Gözlemcilerden hangisinin “doğru”, hangisinin “yanlış” olduğu da söylenemez. Gerçekten de iki gözlemci saatlerini karşılaştırırlarsa, her biri kendi saatinin ötekinin saatinden daha hızlı işlediğini görecektir. Benzer olarak öbür gözlemcinin cetvelinin boyunu da (hareket doğrultusunda olmak üzere) kısalmış bulacaktır.
Özel görelilik kuramının birinci postulası, esirin varlığının ortaya çıkarılamayacağıdır. İkinci postula, hareketli olsun ya da olmasın tüm gözlemcilere göre ışık hızının sabit kalacağıdır. Herhangi bir deneyle esirin varlığı ortaya çıkarılamayacağından, salt elektromagnetik dalgaların taşıyıcısı görevini yüklenmek üzere ortaya atılmış olan bu kavram, çağdaş fizikten tümüyle çıkarılmıştır.
Bir gözlemcinin uzay ve zaman ölçümlerinin, hareketli bir başka gözlemcinin ölçümlerine göre hangi değerleri alacağı, Lorentz dönüşümleri adı verilen matematik denklemleriyle belirlenir. Örneğin x ekseni boyunca ölçülen bağıl hareketin hızı v ise, öteki referans sisteminde,
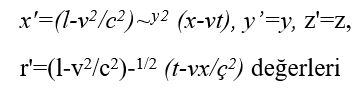 bulunur.
bulunur.Özel kuramın sonuçları
Bir eylemsiz referans sisteminin bir başka referans sistemine göre hızı arttıkça, bu sistemdeki cetveller gitgide kısalır ve saatler gitgide yavaşlar. İki sistemin birbirine göre hızı ışık hızına yaklaştıkça bu etkiler de çok büyük ölçüde artar. Referans sistemlerinin hangisinden bakılırsa bakılsın, ışığın her doğrultudaki hızının c olabilmesi için, iki sistem arasındaki göreli hızın c’den fazla olmaması gerekir. Bu nedenle özel görelilik kuramına göre, referans sistemlerinin göreli hızları c’den büyük olamaz: Lorentz dönüşümleri, bir referans sistemine göre bir cismin hızının, bir başka sistemde alacağı değerleri belirlemiştir. Sistemlerin birbirine göre hızı v, bir sistemdeki cismin hızı u ile gösterilirse, öbür referans sistemine göre cismin
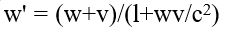 denklemiyle verilir.
denklemiyle verilir.Maddesel bir cismin kütlesi, bir kuvvetin hareket durumunda yol açtığı değişime direncinin bir ölçüsüdür. Cismin kütlesi büyüdükçe ivmesi azalır. Maddesel cismin hızı ışık hızına yaklaştıkça daha fazla hızlanmaya karşı direnci de artar ve bu hız hiçbir zaman c sınırını aşamaz. Özel kurama göre, bir cismin durgun kütlesi m işe, hareketli kütlesi
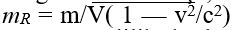 denklemiyle belirlenir. Buna görelilik kütlesi de denir. Cismin kinetik enerjisi E ile gösterilirse, görelilik kütlesi ile durgun kütle arasındaki fark,
denklemiyle belirlenir. Buna görelilik kütlesi de denir. Cismin kinetik enerjisi E ile gösterilirse, görelilik kütlesi ile durgun kütle arasındaki fark, 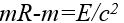 ya da genel olarak
ya da genel olarak 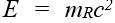 denklemleriyle gösterilir. Bunlar, kütle ile enerjinin eşdeğerliği sonucunu verirler. İki uzak olgu arasındaki zaman aralığı T, bunlar arasındaki uzaklık L olursa tüm eylemsiz referans sistemlerinde aynı değeri alacak olan
denklemleriyle gösterilir. Bunlar, kütle ile enerjinin eşdeğerliği sonucunu verirler. İki uzak olgu arasındaki zaman aralığı T, bunlar arasındaki uzaklık L olursa tüm eylemsiz referans sistemlerinde aynı değeri alacak olan 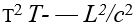 ifadesi yazılabilir. Bu nicelik, bir başka referans sisteminden elde edilen
ifadesi yazılabilir. Bu nicelik, bir başka referans sisteminden elde edilen 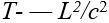 , niceliğine eşittir. Eğer r2 pozitif ise, T niceliğine iki olgu arasındaki değişim- siz (zamansı) aralık adı verilir, T2 negatif ise
, niceliğine eşittir. Eğer r2 pozitif ise, T niceliğine iki olgu arasındaki değişim- siz (zamansı) aralık adı verilir, T2 negatif ise 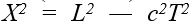 ifadesi türetilebilir ve X niceliğine değişimsiz (uzaysı) aralık denir.
ifadesi türetilebilir ve X niceliğine değişimsiz (uzaysı) aralık denir.Bir eylemsiz referans sistemi ve iki benzer maddesel cisim (ikiz) alınsın. Örneğin, özdeş tasarımlanmış iki atom saatinde, saatlerden biri sistemde sürekli durgun kalırken öbürü ilkin yüksek bir hızla birinciden uzaklaşsın ve sonra gene yüksek hızla geri dönsün. Lorentz dönüşümlerine göre, ikinci saat, yolculuğu süresince daha yavaş işleyeceğinden, döndüğünde birinciye göre geri kalmış olacaktır. Öyleyse saatlere bakılarak hangisinin durgun kalmış, hangisinin hareket etmiş olduğu ayırt edilebilir. Görelilik kuramı farklı eylemsiz referans sistemleri arasında bakışımsız ayrılıklar gözetmediğinden, bu durum görelilik kuramına aykırı gözükmektedir ve “saat paradoksu” ya da “ikiz paradoksu” olarak adlandırılır.
Oysa ikinci saat için aslında bir eylemsiz referans sistemi söz konusu değildir. Çünkü, dönüş yolculuğuna başlayabilmesi için yavaşlaması, durması, ters yönde hareket etmesi ya da bir yay çizerek yön değiştirmesi gerekir. Bütün bu durumlar, ikinci saatin artı ya da eksi ivme kazanması anlamına gelir. Dolayısıyla birinci saat ile aynı eylemsiz referans sisteminde bulunmaz. Bu nedenle görelilik kuramına aykırı bir durum, bir “paradoks” yoktur. Hareketli parçacıklar ve atomlar üzerinde gerçekleştirilen deneyler de kuramı doğrulamaktadır.
Alman matematikçi Hermann Minkowski, iki olgu arasındaki değişimsiz aralığın, Eukleidesçi geometrideki uzaklığın kimi özelliklerine sahip olduğunu gösterdi. Birbirine dikey üç eksenden oluşan kartezyen koordinat sisteminde, iki olgu arasındaki 5 uzaklığı
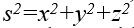 ifadesinin kareköküyle belirlenir ve bu uzaklık koordinat sisteminin seçiminden bağımsızdır. Değişimsiz aralık da, benzer biçimde, uzaydaki ve zamandaki aralıkların karelerinin toplam ve farkının kareköküne eşittir. Minkowski, bu nedenle, uzay ve zamanın tek bir dört boyutlu sürem oluşturduğunu öne sürdü; bu sürem, uzay -zaman ya da Minkowski evreni olarak adlandırılır. Uzay-zamanda değişimsiz aralık zamansı ya da uzaysı olabilir; eğer iki olgu için
ifadesinin kareköküyle belirlenir ve bu uzaklık koordinat sisteminin seçiminden bağımsızdır. Değişimsiz aralık da, benzer biçimde, uzaydaki ve zamandaki aralıkların karelerinin toplam ve farkının kareköküne eşittir. Minkowski, bu nedenle, uzay ve zamanın tek bir dört boyutlu sürem oluşturduğunu öne sürdü; bu sürem, uzay -zaman ya da Minkowski evreni olarak adlandırılır. Uzay-zamanda değişimsiz aralık zamansı ya da uzaysı olabilir; eğer iki olgu için 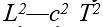 değeri sıfıra eşitse, bu aralık ışıksı olarak adlandırılır, çünkü önceki olgudan çıkan bir ışık ışını, sonraki olgudan tam bu olgu olurken geçer.
değeri sıfıra eşitse, bu aralık ışıksı olarak adlandırılır, çünkü önceki olgudan çıkan bir ışık ışını, sonraki olgudan tam bu olgu olurken geçer.kaynak: Ana Britannica
Son düzenleyen Safi; 16 Ocak 2017 17:23

 Özel Görelilik Kuramı
Özel Görelilik Kuramı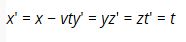
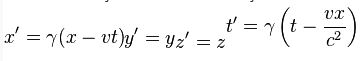
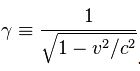 . Lorentz Dönüşümlerinde görüldüğü üzere iki gözlemci için aynı zaman betimlemesi geçerli değildir. Bu dönüşümlerde Einstein'ın Özel Görelilikle ortaya çıkardığı düşünce değişimi görülmektedir, yani farklı hızlardaki iki gözlemci aynı olay için farklı zaman değerleri ölçer.
. Lorentz Dönüşümlerinde görüldüğü üzere iki gözlemci için aynı zaman betimlemesi geçerli değildir. Bu dönüşümlerde Einstein'ın Özel Görelilikle ortaya çıkardığı düşünce değişimi görülmektedir, yani farklı hızlardaki iki gözlemci aynı olay için farklı zaman değerleri ölçer.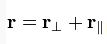
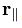 dönüşüme uğrar. O hâlde, Lorentz dönüşümleri
dönüşüme uğrar. O hâlde, Lorentz dönüşümleri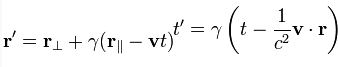 biçimine indirgenmiş olur.
biçimine indirgenmiş olur.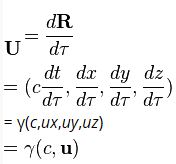
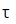 özel zamandır.
özel zamandır.