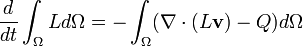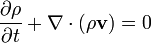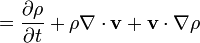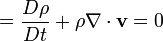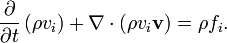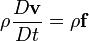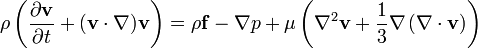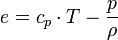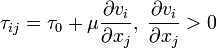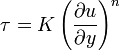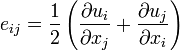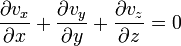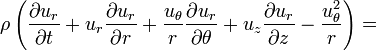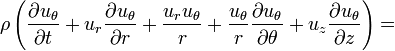Navier-Stokes Denklemleri
VIP VIP Üye
Navier-Stokes Denklemleri
MsXLabs.org & Vikipedi, özgür ansiklopedi
Navier-Stokes denklemleri, ismini Claude-Louis Navier ve George Gabriel Stokes'tan almış olan, sıvılar ve gazlar gibi akışkanların hareketini tanımlamaya yarayan bir dizi denklemden oluşmaktadır.
Bu denklemler; akışkan içerisindeki birim kütleye etki eden momentum (ivmelenme) değişimlerinin, basınç değişimleri ve sürtünme kayıplarına neden olan viskoz kuvvetlerin (sürtünmeye benzer) toplamına eşit olduğunun doğruluğunu ortaya koymaktadır. Bu viskoz kuvvetler moleküller arası etkileşimlerden meydana gelmekte ve akışkanın akmaya ne kadar dirençli (viskoz) olduğunu göstermektedir. Böylece, Navier-Stokes denklemlerinin, verilen akışkanın herhangi bir bölgesindeki kuvvetler dengesinin dinamik ifadesi olduğu söylenebilir.
Bu denklemler en kullanışlı denklemlerin başında gelmektedirler. Çünkü, gerek akademik gerekse ekonomik birçok fenomenin fiziğini açıklamaktadır. Hava akımları ve okyanus akıntılarının, boru içindeki su akışının, galaksideki yıldız hareketlerinin, kanat etrafındaki hava akımlarının modellenmesinde ve hesaplarında sıkça kullanılırlar.
1. Temel kabuller
Navier-Stokes denklemlerinin detayına girmeden önce, akışkanlar hakkında bazı kabuller yapılması gereklidir. Öncelikle akışkanın sürekli olduğu kabul edilir. Yani akışkanın tamamının aynı özellikte olduğu içinde farklı biçimler (formlar) bulunmadığı kabul edilir. Bir başka gerekli kabulde konu ile ilgili tüm alanların basınç, hız, yoğunluk, sıcaklık vs., diferansiyel olduğudur (faz değişimleri olmadan).
Denklemler, momentum ve enerji ve kütle korunumunun temel prensiplerinden elde edilir. Bunun için, bazı hallerde kontrol hacmi adı verilen, rastgele seçilmiş sonlu bir hacim belirlemek gereklidir, bu hacim üzerinde bu prensipler kolayca uygulanabilir. Bu sonlu hacim Ω ile gösterilir ve yüzeyi sınırlandırılır ∂Ω. Kontrol hacmi, sabit kalabilir veya akışkan ile hareket edebilir. Temel kabuller bunlardır, bununla beraber, farklı uygulamalarda özel kabuller de yapılabilir.
2. Gerçek türev
Hareket eden akışkanın özelliklerinin değişiminin ölçülebilmesi için iki yol vardır. Örneğin dünya atmosferindeki rüzgar hızının değişimleri ele alınacak olursa; bu değişiklikler bir meteoroloji istasyonu ölçüm cihazı (anemometre) veya bir hava balonu yolu ile ölçülebilir. Şüphesiz, ilk durumdaki anemometre boşlukta sabit bir nokta boyunca geçiş yapan tüm hareketli parçacıkların hızını ölçerken, ikinci durumda bahsedilen aygıt akışkan ile beraber hareket ederken hızdaki değişimi ölçer.
Aynı durumda, yoğunluk, sıcaklık vb. değişimler de ölçümü etkileyecektir. Bu nedenle, bu iki hal için bir ayırım yapılmalıdır. Bir alanın boşluktaki sabit bir pozisyona göre türevi uzaysal (spatial) veya Euleryen türev (Eulerian derivative) olarak adlandırılır. Hareketli bir parçacığın izlenmesi türevi gerçek (substantive), Lagrangyan (Lagrangian) veya maddi (material) türev olarak adlandırılır.
Gerçek türev şu şekilde tanımlanır:
3. Korunum kanunları
Navier-Stokes denklemleri, aşağıdaki korunum kanunlarından türetilir:
En genel biçimde, bir korunum kanunu şunu ifade eder, bir kontrol hacmi üzerinde tanımlanmış hacim özelliği (bulk property) değişiminin oranı L hacim sınırları boyunca hareket eden akışkanın dışarı taşıdığı kayıp ve artı kontrol hacminin iç tarafındaki kazançlar ve kayıplara eşit kabul edilir. Bu, aşağıdaki integral denklemi ile ifade edilir:
Eğer kontrol hacmi boşluk içinde sabitlenmiş ise bu integral denkleminden aşağıdaki şekilde bir ifade yazılabilir:
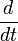" ve "
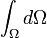" ifadeleri birbirinin yerine yazılabilir. Böylece ifade tüm alanlar için geçerli olur, ve integral çıkartılabilir.
Gerçek türev,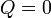
olduğunda (kazanç ve kayıp yokken) elde edilir:
Kütlenin korunumu şu şekilde yazılır:
Sıkıştırılamaz bir akışkan için ρ akış hattı boyunca değişmez ve denklem şu hale indirgenir:
Momentumun korunumu, yoğunluk yerine momentumun vektör bileşenleri ve akışkan üzerine etkiyen kuvvetler ile, süreklilik denklemine benzer bir yaklaşım yapılarak ifade edilir. Süreklilik denkleminde ρ yerine belirli bir yönde birim hacim başına net momentum yazılır.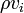
, burada 
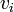hızın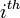 
bileşenidir (hız x, y veya z yönleri boyunca olmak üzere):
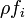, akışkan üzerine etkiyen kuvvetin 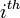bileşenidir (her birim hacim başına gerçek kuvvet). Genel kuvvetler yerçekimi ve basınç gradyenlerini kapsar. Bu şu şekilde de ifade edilebilir:
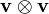bir tensor'dür, 
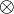tensor çarpımını ifade eder.
Süreklilik denkleminin kullanımı daha da basitleştirilebilir ve şu hale gelir:
4. Denklemler
4.1. Genel biçim
4.1.1. Denklemlerin elde edilişi
Momentumun korunumu için Navier-Stokes denklemlerinin genel biçimi:
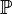tensörü, akışkan parçacığı üzerine uygulanmış yüzey kuvvetleri olarak tanımlanır (gerilme tensörü). Akışkan girdap gibi bağımsız bir eğme bükme hareketi yapmadıkça, 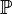simetrik bir tensördür. Genel olarak, biçim:
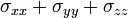matris izi (İng. trace) akışkanın dengede olup, olmadığı mutlaka tanımlanması (hacim vizkozitesi (bulk viscosity) olmadıkça) ile daima -3p'dir.
Sonuç olarak:
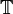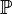, 'nin izsiz (traceless) parçasıdır.
Bu denklemler hala tamamlanmamıştır. Tamamlamak için,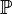'nin şekli üzerinde bir varsayım yapılmalıdır. Şöyle ki, gerilme tensörü için aşağıda gösterildiği gibi bir süreklilik kanununa ihtiyaç vardır.
Akış, sürekli ve diferansiyel kabul edilmiş ve korunum kanunları çerçevesinde kısmi diferansiyel denklemler ile ifade edilmiştir. Akışın sıkıştırılamaz (sabit yoğunluk) olduğu durumda, değişkenler, basınç ve hız bileşenleri için çözülmüştür. Bu değişkenler, Navier-Stokes denklemlerinin üç bileşeni, kütlenin korunumu (süreklilik denklemi) ilave edilerek, kapalı bir sistem için kısmi diferansiyel denklemler ile , sınır şartlarına uygun olarak çözülebilir. Sıkıştırılamaz akış durumunda, yoğunluk sistem için diğer bir bilinmeyen haline gelir, sistem için bir durum denklemi ilavesi ile saptanır. Durum denkleminde genelde akışkanın sıcaklığı işin içine girer, o yüzden denklem enerjinin korunumu için de mutlaka çözülmelidir. Bu denklemler non-lineer'dir (yani lineer değildir) ve kapalı formdaki analitik çözümleri sadece çok basit sınır şartları için bilinir.
Denklemler, akım ve girdap fonksiyonu ikinci değişkenleri için Wilkinson denklemlerine dönüştürülebilirdir. Çözüm akışkan özelliklerine (viskozite, özgül ısı ve ısıl iletkenlik gibi) ve çalışma alanındaki sınır şartlarına bağlıdır.
5. Denklemlerin özel formları
Denklem akışkanlarla ilgili problemlerin çözümü için, genel bazı durumlar için sadeleştirilip, genelleştirilerek kullanılabilir.
5.1. Newtonyen (Newtonian) akışkanlar
Burada ;
Denklem içinde −2/3 ile çarpım görünmesi bununla açıklanır. Bu çarpım, 1 veya 2 uzaysal boyut içinde değiştirilebilir:
Tamamı için yazıldığında, bu karmaşık denklem şu hali alır:
Momentumun korunumu:
Kütlenin korunumu:
Enerjinin korunumu:
Burada:
Ф yüksek süpersonik ve hipersonik uçuşlar gibi sıradışı örnekler hariç, çoğunlukla ihmal edilebilirdir.
İdeal gaz kabul edilir:
5.2. Bingham akışkanları
Bingham akışkanlarında, bazı yerlerde durum biraz daha farklıdır:
5.3. Power-law Akışkanı (Power-law fluid)
Bu akışkan, kesme gerilimi için, ideal hal almış akışkandır, τ şu şekilde verilir:
5.4. Sıkıştırılamaz akışkanlar
Navier-Stokes denklemleri,
Burada
Ek olarak, eğer ρ sabit farzedilirse şu sistem elde edilir:
5.5. Silindirik koordinatlar
Navier-Stokes Süreklilik denklemi silindirik koordinatlar için şöyledir:
r momentum:
MsXLabs.org & Vikipedi, özgür ansiklopedi
Sponsorlu Bağlantılar
Navier-Stokes denklemleri, ismini Claude-Louis Navier ve George Gabriel Stokes'tan almış olan, sıvılar ve gazlar gibi akışkanların hareketini tanımlamaya yarayan bir dizi denklemden oluşmaktadır.
Bu denklemler; akışkan içerisindeki birim kütleye etki eden momentum (ivmelenme) değişimlerinin, basınç değişimleri ve sürtünme kayıplarına neden olan viskoz kuvvetlerin (sürtünmeye benzer) toplamına eşit olduğunun doğruluğunu ortaya koymaktadır. Bu viskoz kuvvetler moleküller arası etkileşimlerden meydana gelmekte ve akışkanın akmaya ne kadar dirençli (viskoz) olduğunu göstermektedir. Böylece, Navier-Stokes denklemlerinin, verilen akışkanın herhangi bir bölgesindeki kuvvetler dengesinin dinamik ifadesi olduğu söylenebilir.
Bu denklemler en kullanışlı denklemlerin başında gelmektedirler. Çünkü, gerek akademik gerekse ekonomik birçok fenomenin fiziğini açıklamaktadır. Hava akımları ve okyanus akıntılarının, boru içindeki su akışının, galaksideki yıldız hareketlerinin, kanat etrafındaki hava akımlarının modellenmesinde ve hesaplarında sıkça kullanılırlar.
1. Temel kabuller
Navier-Stokes denklemlerinin detayına girmeden önce, akışkanlar hakkında bazı kabuller yapılması gereklidir. Öncelikle akışkanın sürekli olduğu kabul edilir. Yani akışkanın tamamının aynı özellikte olduğu içinde farklı biçimler (formlar) bulunmadığı kabul edilir. Bir başka gerekli kabulde konu ile ilgili tüm alanların basınç, hız, yoğunluk, sıcaklık vs., diferansiyel olduğudur (faz değişimleri olmadan).
Denklemler, momentum ve enerji ve kütle korunumunun temel prensiplerinden elde edilir. Bunun için, bazı hallerde kontrol hacmi adı verilen, rastgele seçilmiş sonlu bir hacim belirlemek gereklidir, bu hacim üzerinde bu prensipler kolayca uygulanabilir. Bu sonlu hacim Ω ile gösterilir ve yüzeyi sınırlandırılır ∂Ω. Kontrol hacmi, sabit kalabilir veya akışkan ile hareket edebilir. Temel kabuller bunlardır, bununla beraber, farklı uygulamalarda özel kabuller de yapılabilir.
2. Gerçek türev
Hareket eden akışkanın özelliklerinin değişiminin ölçülebilmesi için iki yol vardır. Örneğin dünya atmosferindeki rüzgar hızının değişimleri ele alınacak olursa; bu değişiklikler bir meteoroloji istasyonu ölçüm cihazı (anemometre) veya bir hava balonu yolu ile ölçülebilir. Şüphesiz, ilk durumdaki anemometre boşlukta sabit bir nokta boyunca geçiş yapan tüm hareketli parçacıkların hızını ölçerken, ikinci durumda bahsedilen aygıt akışkan ile beraber hareket ederken hızdaki değişimi ölçer.
Aynı durumda, yoğunluk, sıcaklık vb. değişimler de ölçümü etkileyecektir. Bu nedenle, bu iki hal için bir ayırım yapılmalıdır. Bir alanın boşluktaki sabit bir pozisyona göre türevi uzaysal (spatial) veya Euleryen türev (Eulerian derivative) olarak adlandırılır. Hareketli bir parçacığın izlenmesi türevi gerçek (substantive), Lagrangyan (Lagrangian) veya maddi (material) türev olarak adlandırılır.
Gerçek türev şu şekilde tanımlanır:
Burada v akışkanın hızıdır. Denklemin sağ tarafındaki ilk terim alışılmış Euleryen türevi (sabit bir referans üzerindeki türev) iken, ikinci terim akışkan hareketi ile oluşan değişiklikleri ifade eder. Bu etki adveksiyon olarak adlandırılır.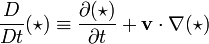
3. Korunum kanunları
Navier-Stokes denklemleri, aşağıdaki korunum kanunlarından türetilir:
- Kütle
- Enerji
- Momentum
- Açısal momentum
En genel biçimde, bir korunum kanunu şunu ifade eder, bir kontrol hacmi üzerinde tanımlanmış hacim özelliği (bulk property) değişiminin oranı L hacim sınırları boyunca hareket eden akışkanın dışarı taşıdığı kayıp ve artı kontrol hacminin iç tarafındaki kazançlar ve kayıplara eşit kabul edilir. Bu, aşağıdaki integral denklemi ile ifade edilir:
Bu denklemde v akışkanın hızı ve Q akışkan içindeki kazançlar ve kayıplar olarak ifade edilir.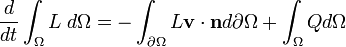
Eğer kontrol hacmi boşluk içinde sabitlenmiş ise bu integral denkleminden aşağıdaki şekilde bir ifade yazılabilir:
Ayrıca, kontrol hacminin içinde, bu son denklemde elde edilmiş olan sağ taraftaki ilk terimin ifade edilmesi için diverjans teoremi kullanılmıştır. Böylece: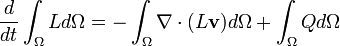
Yukarıdaki ifade boşlukta sabit kalan bir kontrol hacminde Ω için geçerlidir. Çünkü Ω zaman içinde sabittir, değişmez. Bu sayede "
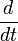" ve "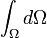" ifadeleri birbirinin yerine yazılabilir. Böylece ifade tüm alanlar için geçerli olur, ve integral çıkartılabilir.Gerçek türev,
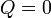olduğunda (kazanç ve kayıp yokken) elde edilir:3.1. Süreklilik denklemi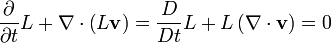
Kütlenin korunumu şu şekilde yazılır:
Burada ρ kütle yoğunluğu (birim hacim başına kütle), v akışkanın hızıdır.
Sıkıştırılamaz bir akışkan için ρ akış hattı boyunca değişmez ve denklem şu hale indirgenir:
3.2. Momentumun korunumu
Momentumun korunumu, yoğunluk yerine momentumun vektör bileşenleri ve akışkan üzerine etkiyen kuvvetler ile, süreklilik denklemine benzer bir yaklaşım yapılarak ifade edilir. Süreklilik denkleminde ρ yerine belirli bir yönde birim hacim başına net momentum yazılır.
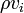, burada 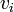hızın 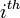bileşenidir (hız x, y veya z yönleri boyunca olmak üzere):
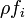, akışkan üzerine etkiyen kuvvetin 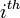bileşenidir (her birim hacim başına gerçek kuvvet). Genel kuvvetler yerçekimi ve basınç gradyenlerini kapsar. Bu şu şekilde de ifade edilebilir:Ayrıca,
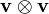bir tensor'dür, 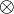tensor çarpımını ifade eder.Süreklilik denkleminin kullanımı daha da basitleştirilebilir ve şu hale gelir:
Genel kullanımda aşağıdaki gibi de yazılabilir: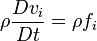
Bu bağlamda F=ma ifadesi doğrulanmış olur.
4. Denklemler
4.1. Genel biçim
4.1.1. Denklemlerin elde edilişi
Momentumun korunumu için Navier-Stokes denklemlerinin genel biçimi:
Burada ρ akışkan yoğunluğu, v hız vektörü ve f kitle kuvvet vektörüdür.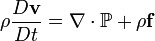
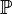tensörü, akışkan parçacığı üzerine uygulanmış yüzey kuvvetleri olarak tanımlanır (gerilme tensörü). Akışkan girdap gibi bağımsız bir eğme bükme hareketi yapmadıkça, 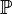simetrik bir tensördür. Genel olarak, biçim:Burada σ normal gerilmeler, τ teğetsel gerilmeler (kesme gerilmeleri) ve p gerilme tensörünün izotropik parçası ile birleştirilmiş statik basınçtır.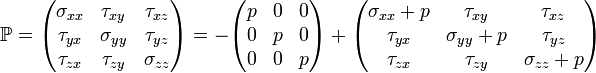
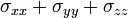matris izi (İng. trace) akışkanın dengede olup, olmadığı mutlaka tanımlanması (hacim vizkozitesi (bulk viscosity) olmadıkça) ile daima -3p'dir.Sonuç olarak:
Burada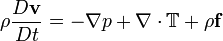
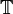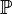, 'nin izsiz (traceless) parçasıdır.Bu denklemler hala tamamlanmamıştır. Tamamlamak için,
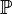'nin şekli üzerinde bir varsayım yapılmalıdır. Şöyle ki, gerilme tensörü için aşağıda gösterildiği gibi bir süreklilik kanununa ihtiyaç vardır.Akış, sürekli ve diferansiyel kabul edilmiş ve korunum kanunları çerçevesinde kısmi diferansiyel denklemler ile ifade edilmiştir. Akışın sıkıştırılamaz (sabit yoğunluk) olduğu durumda, değişkenler, basınç ve hız bileşenleri için çözülmüştür. Bu değişkenler, Navier-Stokes denklemlerinin üç bileşeni, kütlenin korunumu (süreklilik denklemi) ilave edilerek, kapalı bir sistem için kısmi diferansiyel denklemler ile , sınır şartlarına uygun olarak çözülebilir. Sıkıştırılamaz akış durumunda, yoğunluk sistem için diğer bir bilinmeyen haline gelir, sistem için bir durum denklemi ilavesi ile saptanır. Durum denkleminde genelde akışkanın sıcaklığı işin içine girer, o yüzden denklem enerjinin korunumu için de mutlaka çözülmelidir. Bu denklemler non-lineer'dir (yani lineer değildir) ve kapalı formdaki analitik çözümleri sadece çok basit sınır şartları için bilinir.
Denklemler, akım ve girdap fonksiyonu ikinci değişkenleri için Wilkinson denklemlerine dönüştürülebilirdir. Çözüm akışkan özelliklerine (viskozite, özgül ısı ve ısıl iletkenlik gibi) ve çalışma alanındaki sınır şartlarına bağlıdır.
5. Denklemlerin özel formları
Denklem akışkanlarla ilgili problemlerin çözümü için, genel bazı durumlar için sadeleştirilip, genelleştirilerek kullanılabilir.
5.1. Newtonyen (Newtonian) akışkanlar
Burada ;
- μ, akışkanın vizkozitesidir.
- δij, ise Kronecker delta olarak adlandırılan matematik işlemini ifade eder (1 için i=j; 0 için i ≠ j).
pij=-pδijNewtonyen bir akışkan için, bu denge değerinden gerilim tensörünün sapması, hızın gradyeni içinde lineerdir. Galile sabiti (Galilean covariance) nedeni ile açık şekilde hız üzerinde bağımlı değildir. Diğer bir ifade ile pij=-pδij, ∂ivj de lineerdir. Akışkanların dönme sabiti belirlenir (sıvı kristal (liquid crystal) olmayanlar). pij+pδij izli ve izsiz simetrik tensörlerine ayrılır. Benzer olarak ∂ivj izli, izsiz simetrik ve antisimetrik tensorlere ayrılır. Antisimetrik parça sıfıra gider, izli parça ve izsiz simetrik parçaya uygun iki katsayı vardır. ∂ivj'nin izsiz simetrik parçası,
Burada d uzaysal ölçü sayısıdır ve izli parça δij∂kvk'dır. Bu nedenle, en genel lineer dönme sabiti şu şekilde verilir:'dir.
μ ve μB bazı katsayılardır. μ kesme vizkozitesi (shear viscosity) ve μB hacim vizkozitesi (bulk viscosity) olarak adlandırılır. Bu ampirik (deneysel) bir incelemedir, hacim vizkozitesi çoğu akışkan için ihmal edilebilirdir, bu nedenle çoğu zaman ihmal edilir.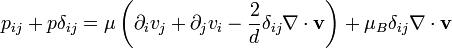
Denklem içinde −2/3 ile çarpım görünmesi bununla açıklanır. Bu çarpım, 1 veya 2 uzaysal boyut içinde değiştirilebilir:
Burada, Einstein notasyonu kullanılmıştır.
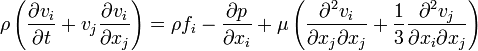
Tamamı için yazıldığında, bu karmaşık denklem şu hali alır:
Momentumun korunumu:
Kütlenin korunumu:
Yoğunluk bilinmediği zaman, diğer bir denklem gereklidir.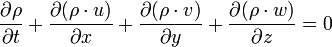
Enerjinin korunumu:
Burada:
Ф yüksek süpersonik ve hipersonik uçuşlar gibi sıradışı örnekler hariç, çoğunlukla ihmal edilebilirdir.
İdeal gaz kabul edilir:
Altı bilinmeyen (u, v, w, T, e ve ρ) ve altı denklemden oluşan yukarıdaki gibi bir çözüm sistemi elde edilmiş olur.
5.2. Bingham akışkanları
Bingham akışkanlarında, bazı yerlerde durum biraz daha farklıdır:
Bunlar, akış başlamadan önce bir miktar kesme dayanım kabiliyetleri olan akışkanlardır. Örnek olarak, diş macunu verilebilir.
5.3. Power-law Akışkanı (Power-law fluid)
Bu akışkan, kesme gerilimi için, ideal hal almış akışkandır, τ şu şekilde verilir:
Bu form, hemen hemen genel akışkanların tüm çeşitlerine uygulanır.
5.4. Sıkıştırılamaz akışkanlar
Navier-Stokes denklemleri,
momentumun korunumu ve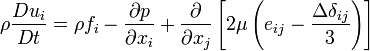
kütlenin korunumu için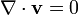
Burada
- ρ=yoğunluk,
- ui= (i =1, 2, 3) hızın üç bileşeni,
- fi= gövde kuvvetleri (yerçekimi gibi),
- p= basınç,
- μ= akışkanın o noktadaki dinamik vizkozitesi;
- ∆= eii; diverjans
- δij; Kronecker delta
(Eğer μ=0 fakat akışkan sıkıştırılabilir ise sonuçta Euler denklemleri olarak bilinen denklemler elde edilir; burada , önemli olan sıkıştırılabilir akış ve akış içindeki şok dalgalarıdır.)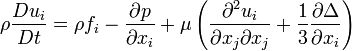
Ek olarak, eğer ρ sabit farzedilirse şu sistem elde edilir:
Süreklilik denklemi (sıkıştırılamazlık kabulu ile):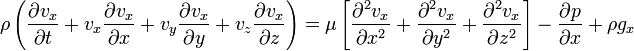
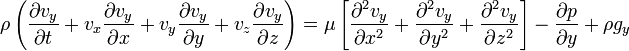
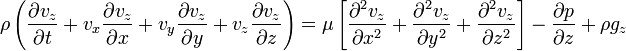
5.5. Silindirik koordinatlar
Navier-Stokes Süreklilik denklemi silindirik koordinatlar için şöyledir:
Silindirik koordinatlar için Navier-Stokes denklemleri de şu şekilde yazılır:=0
r momentum:
θ momentum:
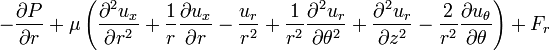
z momentum:
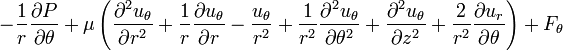
Şunu ifade etmek gerekir ki, Navier-Stokes denklemleri akışkan akışını sadece yaklaşık olarak tanımlayabilir ve çok küçük ölçeklerde veya sıradışı şartlarda, gerçek akışkanlar diğer maddeleri ve molekülleri içeren karışımlardır, Navier-Stokes denklemleri ile homojen ve sürekli akışlar modellenmiş ve bunun üzerinden sonuçlar elde edilmiştir. Bununla beraber Navier-Stokes denklemleri pratikteki problemlerin çözümü için, geniş bir aralıkta faydalı olur.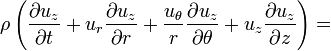
Tanrı varsa eğer, ruhumu kutsasın... Ruhum varsa eğer!
