Sıralamalar
Ziyaretçi
Bir küme ve o küme üzerinde aşağıda tarif edilecek olan ikili bir ilişki içeren aksiyomatik sistemlere denir. Bilinen sıralama 
ilişkisinin soyutlanmasıyla elde edilirler. Kümemize X, ilişkimize R adını verecek olursak, aşağıdaki aksiyomların sağlandığını varsayarız.
Doğal Sayılar, ilişkisi) -- (Rasyonel Sayılar, ilişkisi) -- (Reel Sayılar, ilişkisi) -- (Kümeler Uzayı*, 
ilişkisi)
* Teknik olarak bir küme değildir ancak bu sorun yaratmaz.
Sıralama Çeşitleri
Vikipedi, özgür ansiklopedi
ilişkisinin soyutlanmasıyla elde edilirler. Kümemize X, ilişkimize R adını verecek olursak, aşağıdaki aksiyomların sağlandığını varsayarız.- X kümesinin her a elemanı için R(a,a) ilişkisi sağlanmalıdır. (
şeklinde düşünülebilir, yansıma özelliği olarak bilinir.)
- X kümesinin herhangi iki a ve b elemanı için R(a,b) ve R(b,a) ilişkileri sağlanıyorsa, a = b olamlıdır. (hem
hem de 
sağlanıyorsa a=b dir diye düşünülebilir, antisimetrik olma özelliği olarak bilinir.)
- X kümesinin herhangi üç a, b, ve c elemanı için hem R(a,b) hem de R(b,c) ilişkileri ağlanıyorsa, o zaman R(a,c) ilişkisi de sağlanmalıdır. (hem
ise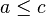 
de olmalıdır diye de düşünülebilir, geçişkenlik özelliği olarak bilinir) hem de
Sponsorlu Bağlantılar
ilişkisi) -- (Rasyonel Sayılar, ilişkisi) -- (Reel Sayılar, ilişkisi) -- (Kümeler Uzayı*, ilişkisi)* Teknik olarak bir küme değildir ancak bu sorun yaratmaz.
Sıralama Çeşitleri
- Eğer elimizdeki sıralama nesnesi, yukardaki aksiyomlara ek başka varsayımlar sağlamıyorsa elimizdeki sıralamaya "kısmi sıralama" denir. Yani her sıralama bir kısmi sıralamadır.
- Eğer yukardaki aksiyomlara ek olarak X ten seçeceğimiz herhangi iki elemanı karşılaştırabiliyorsak (yani R(a,b) ve R(b,a) ilişkilerinden biri mutlaka doğru olmak zorundaysa) o zaman elimizdeki sıralamaya doğrusal sıralama denir. Yukardaki örneklerden (Doğal Sayılar, ), (Rasyonel Sayılar, ) ve (Reel Sayılar, ) aynı zamanda doğrusal sıralamalara da örneklerken, (Kümeler Uzayı, ilişkisi), doğrusal olmayan kısmi bir sıralamadır. Nedeni herhangi iki kümeyi ilişkisine göre karşılaştırmanın mümkün olmamasıdır. Yani biri diğerini içermeyen iki kümenin varlığıdır.
- Son olarak, doğrusal sıralama şartlarını sağlayan (X, R) sırlamalarından, "X in her alt kümesinin bir en küçük eleman içermesi şartı"nı sağlayanlara iyi-sıralama denir. Yukardaki örneklerden reel sayılar ve doğal sayılar iyi-sıralamalarken, rasyonel sayılar iyi sıralama değildir. Örnek olarak "karekök ikiden büyük rasyonel sayılar" kümesinin en küçük bir elemanı olmaması verilebilir.
- Her sıralama nesnesi bir topolojik uzay yapısına sahiptir. Bu yapının açık kümelerinin temeli "öyle x elemanları ki
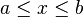" şeklinde ifade edilebilen kümelerden oluşur, a veya b az önceki formülde gözükmüyor da olabilirler.
- Zorn'un Lemması, sayesinde kısmi sıralamalar matematiğin pek çok alanında uygulama bulmuşlardır. Mesela halka'larda maksimal ideallerin varlığı Zorn'un Lemması ve ideallarin ilişkisine göre kısmi bir sıralama oluşturduğu gerçeği kullanılarak ispatlanır.
- Reel Sayılar Kümesi'nin Rasyonel Sayılar Kümesi'ni kullanılarak oluşturulmasının bir temeli de Alman matematikçi Richard Dedekindbütünleme"dir. tarafından verilmiştir. Dedekind'in yöntemi Rasyonel Sayılar Kümesi'nin bir iyi-sıralama haline getirilmesine dayanır. Diğer yöntem ise "
- İyi sıralamar matematikte nispeten nadir gözlenen, çok güçlü özellikler içeren objelerdir. Bu ilke ve kümeler teorisi arasındaki ilişki hakkında bilgi için ayrica İyi-sıralılık ilkesi Makalesi'ne bakabilirsiniz.
Vikipedi, özgür ansiklopedi
