Ziyaretçi
Kutupsal denklemler
Kutupsal koordinatlar ile ifade edilmiş bir eğri denklemi "kutupsal denklem" olarak bilinir ve genellikle r, θ'nın bir fonksiyonu olarak yazılır.
Kutupsal denklemler değişik simetri biçimleri gösterebilir. Bir eğri,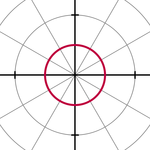
r(θ) = 1 denklemi ile verilmiş çember
Çember
Merkezi (r0, φ) noktasında ve yarıçapı a olan herhangi bir çemberin genel denklemi şu şekildedir:
 Bu denklem özel durumlar için çeşitli yollarla basitleştirilebilir. Örneğin
Bu denklem özel durumlar için çeşitli yollarla basitleştirilebilir. Örneğin
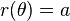 , merkezi kutup noktasında ve yarıçapı a olan çember için yazılmış denklemdir.
, merkezi kutup noktasında ve yarıçapı a olan çember için yazılmış denklemdir.
Doğru
Kutuptan geçen ışınsal doğrular şu denklemle gösterilir:
 Burada φ, doğrunun eğim açısıdır ve m'nin Kartezyen koordinat sistemindeki eğimi temsil ettiği
Burada φ, doğrunun eğim açısıdır ve m'nin Kartezyen koordinat sistemindeki eğimi temsil ettiği
 denklemi ile de ifade edilebilir.
denklemi ile de ifade edilebilir.
Kutup noktasından geçmeyen herhangi bir doğru, ışınsal bir doğruya diktir.θ = φ doğrusunu (r0, φ) noktasında dik kesen doğrunun denklemi ise şöyledir:
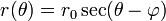 .
. 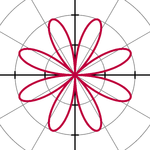
r(θ) = 2 sin 4θ denklemi ile verilmiş kutupsal gül şekli.
Kutupsal gül
Kutupsal gül, taç yapraklı bir çiçeği andıran ve sadece kutupsal bir denklem ile ifade edilebilen ünlü bir matematiksel eğridir. Şu denklemlerle tanımlanır:
 VEYA
VEYA . a değişkeninin gülün yapraklarının uzunluğunu ifade ettiği bu denklemlerde eğer k bir tamsayı ise, k tek sayı olduğunda bu denklemler ile k-yapraklı bir gül ve çift sayı olduğundaysa 2k-yapraklı bir gül elde edilir. Eğer k tam sayı değilse, yaprak sayısı da tamsayı olmayacağı için, bir daire şekli oluşur. Dikkat edilmesi gereken nokta, bu denklemlerle 4'ün katlarının 2 fazlası (2, 6, 10, 14, ...) kadar sayıda taç yaprak elde etmenin mümkün olmadığıdır.
. a değişkeninin gülün yapraklarının uzunluğunu ifade ettiği bu denklemlerde eğer k bir tamsayı ise, k tek sayı olduğunda bu denklemler ile k-yapraklı bir gül ve çift sayı olduğundaysa 2k-yapraklı bir gül elde edilir. Eğer k tam sayı değilse, yaprak sayısı da tamsayı olmayacağı için, bir daire şekli oluşur. Dikkat edilmesi gereken nokta, bu denklemlerle 4'ün katlarının 2 fazlası (2, 6, 10, 14, ...) kadar sayıda taç yaprak elde etmenin mümkün olmadığıdır.

0 < θ < 6π için r(θ) = θ denklemi ile verilmiş Arşimet spiralinin bir kolu.
Arşimet spirali
Arşimet spirali, Arşimet tarafından keşfedilmiş ve gene yalnızca bir kutupsal denklem ile tanımlanabilen, ünlü bir spiraldir. Şu denklemle ifade edilir:
 . a değişkeninin değişimi spirali döndürürken, b değişkeni spiralin kolları arasındaki daima sabit olan uzaklığı kontrol eder. Arşimet spirali, θ > 0 ve θ < 0 değerleri için iki kola sahiptir. İki kol kutup noktasında birbirine düzgün biçimde bağlanır. Kollardan birinin 90°/270° doğrusu üzerinden ayna simetrisi alınırsa, diğer kol elde edilir.
. a değişkeninin değişimi spirali döndürürken, b değişkeni spiralin kolları arasındaki daima sabit olan uzaklığı kontrol eder. Arşimet spirali, θ > 0 ve θ < 0 değerleri için iki kola sahiptir. İki kol kutup noktasında birbirine düzgün biçimde bağlanır. Kollardan birinin 90°/270° doğrusu üzerinden ayna simetrisi alınırsa, diğer kol elde edilir.
Konik kesitler

Semi-latus rectum mesafesinin gösterildiği bir elips
Büyük ekseni kutupsal eksen (0° ışını) üzerinde, bir odağı kutup noktasında ve diğer odağı da kutupsal eksen üzerindeki başka bir noktada bulunan bir konik kesit şu kutupsal denklem ile tanımlanır:
 . Burada e eksantriklik ve l de (semi-latus rectum) büyük eksene dik olarak bir odaktan eğriye kadar ölçülen uzaklıktır. Denklem; e >; 1 ise bir hiperbol, e = 1 ise bir parabol ve e < 1 ise bir elips oluşturur. e < 1 koşulunun özel bir durumu olarak e = 0 ise, yarıçapı l olan bir çember elde edilir.
. Burada e eksantriklik ve l de (semi-latus rectum) büyük eksene dik olarak bir odaktan eğriye kadar ölçülen uzaklıktır. Denklem; e >; 1 ise bir hiperbol, e = 1 ise bir parabol ve e < 1 ise bir elips oluşturur. e < 1 koşulunun özel bir durumu olarak e = 0 ise, yarıçapı l olan bir çember elde edilir.
Diğer eğriler
Kutupsal koordinat sisteminin dairesel özelliği, birçok eğrinin Kartezyen biçimdense kutupsal bir denklemle çok daha kolay tanımlanmasını sağlar. Bu eğrilerin arasında lemniskatlar, ilmek eğrileri (limaçonlar) ve özel bir tip limaçon olan kardiyoidler vardır.
Sponsorlu Bağlantılar
Kutupsal denklemler değişik simetri biçimleri gösterebilir. Bir eğri,
- eğer r(−θ) = r(θ) ise 0°/180° yatay ışınına göre,
- eğer r(π−θ) = r(θ) ise 90°/270° dikey ışınına göre ve
- eğer r(θ−α) = r(θ) ise saat yönünün tersinde, rotasyonel (dönel) olarak kutup noktasına göre α° kadar simetrik olacaktır.

r(θ) = 1 denklemi ile verilmiş çember
Çember
Merkezi (r0, φ) noktasında ve yarıçapı a olan herhangi bir çemberin genel denklemi şu şekildedir:
 Bu denklem özel durumlar için çeşitli yollarla basitleştirilebilir. Örneğin
Bu denklem özel durumlar için çeşitli yollarla basitleştirilebilir. Örneğin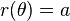 , merkezi kutup noktasında ve yarıçapı a olan çember için yazılmış denklemdir.
, merkezi kutup noktasında ve yarıçapı a olan çember için yazılmış denklemdir.Doğru
Kutuptan geçen ışınsal doğrular şu denklemle gösterilir:
 Burada φ, doğrunun eğim açısıdır ve m'nin Kartezyen koordinat sistemindeki eğimi temsil ettiği
Burada φ, doğrunun eğim açısıdır ve m'nin Kartezyen koordinat sistemindeki eğimi temsil ettiği denklemi ile de ifade edilebilir.
denklemi ile de ifade edilebilir.Kutup noktasından geçmeyen herhangi bir doğru, ışınsal bir doğruya diktir.θ = φ doğrusunu (r0, φ) noktasında dik kesen doğrunun denklemi ise şöyledir:
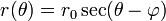 .
. 
r(θ) = 2 sin 4θ denklemi ile verilmiş kutupsal gül şekli.
Kutupsal gül
Kutupsal gül, taç yapraklı bir çiçeği andıran ve sadece kutupsal bir denklem ile ifade edilebilen ünlü bir matematiksel eğridir. Şu denklemlerle tanımlanır:
 VEYA
VEYA . a değişkeninin gülün yapraklarının uzunluğunu ifade ettiği bu denklemlerde eğer k bir tamsayı ise, k tek sayı olduğunda bu denklemler ile k-yapraklı bir gül ve çift sayı olduğundaysa 2k-yapraklı bir gül elde edilir. Eğer k tam sayı değilse, yaprak sayısı da tamsayı olmayacağı için, bir daire şekli oluşur. Dikkat edilmesi gereken nokta, bu denklemlerle 4'ün katlarının 2 fazlası (2, 6, 10, 14, ...) kadar sayıda taç yaprak elde etmenin mümkün olmadığıdır.
. a değişkeninin gülün yapraklarının uzunluğunu ifade ettiği bu denklemlerde eğer k bir tamsayı ise, k tek sayı olduğunda bu denklemler ile k-yapraklı bir gül ve çift sayı olduğundaysa 2k-yapraklı bir gül elde edilir. Eğer k tam sayı değilse, yaprak sayısı da tamsayı olmayacağı için, bir daire şekli oluşur. Dikkat edilmesi gereken nokta, bu denklemlerle 4'ün katlarının 2 fazlası (2, 6, 10, 14, ...) kadar sayıda taç yaprak elde etmenin mümkün olmadığıdır.
0 < θ < 6π için r(θ) = θ denklemi ile verilmiş Arşimet spiralinin bir kolu.
Arşimet spirali
Arşimet spirali, Arşimet tarafından keşfedilmiş ve gene yalnızca bir kutupsal denklem ile tanımlanabilen, ünlü bir spiraldir. Şu denklemle ifade edilir:
 . a değişkeninin değişimi spirali döndürürken, b değişkeni spiralin kolları arasındaki daima sabit olan uzaklığı kontrol eder. Arşimet spirali, θ > 0 ve θ < 0 değerleri için iki kola sahiptir. İki kol kutup noktasında birbirine düzgün biçimde bağlanır. Kollardan birinin 90°/270° doğrusu üzerinden ayna simetrisi alınırsa, diğer kol elde edilir.
. a değişkeninin değişimi spirali döndürürken, b değişkeni spiralin kolları arasındaki daima sabit olan uzaklığı kontrol eder. Arşimet spirali, θ > 0 ve θ < 0 değerleri için iki kola sahiptir. İki kol kutup noktasında birbirine düzgün biçimde bağlanır. Kollardan birinin 90°/270° doğrusu üzerinden ayna simetrisi alınırsa, diğer kol elde edilir.Konik kesitler

Semi-latus rectum mesafesinin gösterildiği bir elips
Büyük ekseni kutupsal eksen (0° ışını) üzerinde, bir odağı kutup noktasında ve diğer odağı da kutupsal eksen üzerindeki başka bir noktada bulunan bir konik kesit şu kutupsal denklem ile tanımlanır:
 . Burada e eksantriklik ve l de (semi-latus rectum) büyük eksene dik olarak bir odaktan eğriye kadar ölçülen uzaklıktır. Denklem; e >; 1 ise bir hiperbol, e = 1 ise bir parabol ve e < 1 ise bir elips oluşturur. e < 1 koşulunun özel bir durumu olarak e = 0 ise, yarıçapı l olan bir çember elde edilir.
. Burada e eksantriklik ve l de (semi-latus rectum) büyük eksene dik olarak bir odaktan eğriye kadar ölçülen uzaklıktır. Denklem; e >; 1 ise bir hiperbol, e = 1 ise bir parabol ve e < 1 ise bir elips oluşturur. e < 1 koşulunun özel bir durumu olarak e = 0 ise, yarıçapı l olan bir çember elde edilir.Diğer eğriler
Kutupsal koordinat sisteminin dairesel özelliği, birçok eğrinin Kartezyen biçimdense kutupsal bir denklemle çok daha kolay tanımlanmasını sağlar. Bu eğrilerin arasında lemniskatlar, ilmek eğrileri (limaçonlar) ve özel bir tip limaçon olan kardiyoidler vardır.
Son düzenleyen asla_asla_deme; 11 Nisan 2012 11:24
Sebep: Sayfa Düzeni / Kaynak Vikipedi

 Kutupsal Denklemler
Kutupsal Denklemler
