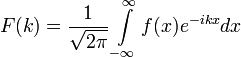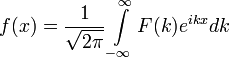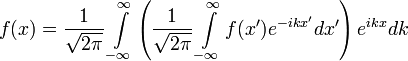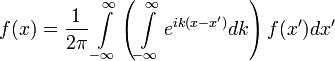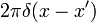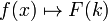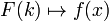Fourier Dönüşümü

Fourier Dönüşümü
MsXLabs.org & Vikipedi, özgür ansiklopedi

Sponsorlu Bağlantılar

Fourier dönüşümü, sürekli ve ayrık olarak ikiye ayrılabilir. İki dönüşüm de bir nesneyi ortogonal iki uzay arasında eşler.
Sürekli nesneler için dönüşüm;

ve

şeklinde verilir. Yukarıdaki dönüşümde görüleceği üzere x uzayındaki bir nesne k uzayında tanımlanmıştır. Bu dönüşüm diferansiyel denklemlerin çözümünde çok büyük rahatlık sağlar zira bu dönüşüm sayesinde x uzayındaki diferansiyel denklemler k uzayında lineer denklemler olarak ifade edilirler. K uzayında bu denklemin çözümü bulunduktan sonra ters dönüşümle x uzayındaki karşılığı elde edilir, ki bu diferansiyel denklemin çözümüdür. Birinci dönüşümdeki ifade ikinci dönüşümde yerine oturtularak,

ifadesine ulaşılır. Parantez içindeki ifadenin

olduğu görülebilir. Anlaşıldığı üzere

eşlemesine Fourier Dönüşümü,

eşlemesine de Ters Fourier Dönüşümü denir ve bu eşlemeler (mapping) yapılırken baş harfleri büyük yazılarak gösterilir (FD ve TFD). Parantez içindeki ifadenin Delta fonksiyonunun temsili olması ise açıkça bir düz ve bir ters Fourier dönüşümü yapılan bir ifadenin kendine eşit olmasından kaynaklanır. Dönüşüm uzayları keyfi seçilebilir ancak fizikte, konum uzayından momentum uzayına ve zaman uzayından enerji uzayına De Broglie-Einstein denklemleriyle geçişler tanımlanmıştır.

Fourier Analizi ve Dönüşümü!

Dalga paketleri ve sinyaller çok sayıda dalganın üst üste binmesinden oluşabilir. Fourier analizinde ise oluşum ters yönde ele alınıp incelenir. Yani matematiksel formülü verilen bir bileşke dalganın, bir sinyalin hangi bileşen dalgalardan oluştuğu Fourier analizi yöntemi ile anlaşılır.

Fourier analizi, öncelikle periyodik herhangi bir fonksiyonu basit sinüs ve kosinüsler toplamı biçiminde yazma esasına dayanıyordur. Karmaşık bir fonksiyon Fourier analizi aracılığıyla bileşenlerine ayrılıp, analiz edilebilir.

Gelişen elektronik sanayii içerisinde Fourier analizi yapan elektronik aletler (analizörler) ve hatta bilgisayar programları yardımı ile herhangi bir karmaşık periyodik fonksiyon Fourier bileşenlerine kolayca ayrılabilmektedir.

Bir fonksiyonun Fourier serisine açılabilmesi için belli bazı matematiksel şartları (Dirichlet şartlarını) sağlaması gerekir. Bu bağlamda Fourier analizinin yanında Fourier dönüşümüne gerek duyulur.

Fourier dönüşümü, verilen bir fonksiyonun Fourier analizini yaparken, fonksiyonun verildiği uzayda değil de başka bir uzayda incelenmesi olarak bilinir. Örneğin ilgili fonksiyonu t=zaman uzayında değil de dalga=frekans uzayında incelemek, analiz etmek fiziksel açıdan daha anlamlıdır. Bu gibi durumlarda olayın incelendiği uzayı (domain) değiştirmek gerekir. Söz konusu durum bir nevi değişken değiştirmek demektir. Fourier dönüşümü ise bu temel mantık üzerine kuruludur.