Matematik bilimi içinde moment kavramı fizik] bilimi için ortaya çıkartılmış olan moment kavramından geliştirilmiştir. Bir bir reel değişkenin reel-değerli fonksiyon olan f(x)in c değeri etrafında ninci momenti şöyle ifade edilir:
 Sıfır değeri etrafında olan momentler en basit olarak bir fonksiyonun momenti diye anılır.
Sıfır değeri etrafında olan momentler en basit olarak bir fonksiyonun momenti diye anılır.
Olasılık kuramı ve istatistik bilim dalları için momentlerin ilgili olduğu fonksiyonlar bir rassal değişken için olasılık yoğunluk fonksiyonu ile ilgilidir. Bir olasılık yogunluk fonksiyonun sıfır etrafındaki ninci momenti Xnin matematiksel beklentidir. Ortalama μ etrafındaki momentler merkezsel momentler olarak adlandırılır; bunlar bir fonksiyonun şekilini betimlerler.
Eğer f bir olasılık yoğunluk fonksiyonu ise, o halde yukarıda verilmiş olan entegralin değeri olasılık dağılımınin ninci moment Riemann-Stieltjes entegrali tarafından şöyle verilir:
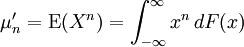
Burada X bu dağılımı gösteren bir rassal değişken ve E bir beklenti operatörüdür.
Eğer
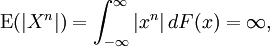
ise momentin mevcut olmadığı kabul edilir. Egğr herhangi bir nokta etrafında ninci moment belirlenebilirse, o halde (n − 1)inci moment de bulunur ve her bir nokta etrafında daha-alt derecelerdeki momentler de bulunur.
Momentlerin Önemi
Sıfır etrafindaki birince moment, eğer anlamlı ise, Xin matematiksel beklentisi yani μ olarak yazilan Xin olasılık dağılımının ortalamasıdır. Daha yüksek dereceler icin merkezsel momentler sıfır etrafında momentlerden daha ilgi çekicidir.
Bir rassal değişken olan Xin olasılık dağılımının ninci merkezsel momenti şudur:
 Böylece birinci merkezsel moment 0 olur.
Böylece birinci merkezsel moment 0 olur.
Varyans
İkinci merkezsel moment varyans σ2 olur; bunun pozitif kare kökü standart sapma σ olur.
Normalize edilmiş momentler
Normalize edilmis ninci merkezsel moment veya standardize edilmis moment ninci merkezsel moment bolu σn olur; yani t = (x − μ)/σ ifadesinin ninci momentidir. Bu normalize edilmis momentler boyutsuz niceliklerdir ve herhangi bir dogrusal iskala degisiminden etkilenmeden bir dagilimi temsil edebilirler.
Çarpıklık
Üçüncü merkezsel moment bir dağılımın simetrik olmaması ölçüsüdür. Herhangi bir simetrik dağılım için üçüncü merkezsel moment, eğer tanımlanabilirse, 0 olur. Normalize edilmiş üçüncü merkezsel moment γ ile yazılıp çarpıklık adı ile anılır. Sol tarafa çarpıklık gösteren (yani sol kuyruğu daha ağır basan) bir dağılım negatif çarpıklık gösterir. Sağ tarafa çarpıklık gösteren (yani sağ kuyruğu daha ağır basan) bir dağılım pozitif çarpıklık gösterir.
Normal dağılımdan çok fazla farklı olmayan dağılımlar icin medyan μ − γσ/6 değerine yaklasik olur ve mod ise μ − γσ/2 ifadesine yaklaşıktır.
Basıklık
Dorduncu merkezsel moment dagilimin ince ve sivri mi yoksa kalin ve basik mi oldugunun olcusudur ve bu niteligi ayirt etmek icin ayni varyansi gosteren bir normal dagilim ile karsilastirma yapilir. Dorduncu merkezsel moment, bir dortlu ustelin matematiksel beklentisi oldugu icin, eger tanimi yapilabilirse, (sadece dejenere nokta dagilim haric) her zaman pozitif deger alir. Bir normal dagilim icin dorduncu merkezsel moment 3σ4 olur.
Basıklık olcusu olarak kullanilan basıklık fazlalığı katsayisi κ, normalize edilmis dorduncu merkezsel moment eksi 3 olarak tanimlanir. (Gelecek kisimda gosterildigi gibi, bu olcu dorduncu kümülant bolu varyans kare olarak da tanimlanir.) Bazi otoriteler bu sekilde normal dagilimi koordinatlarin orijinine koymak icin kullanilan eksi 3 terimini tenkit etmektedirler. Eger bir dagilim aortalama degerinde bir doruk ve iki tarafinda uzun kuyruklara gosterirse, dorduncu moment degeri buyuk olur ve basiklik olcusu κ pozitifdir; aksi halde dorduncu moment degeri kucuk ve basiklik olcusu κ negatif olur. Boylece sinirlanmis dagilimlarda basiklik dusuktur.
Basıklık olcusu hic sinirsiz bir sekilde pozitif olmasi mumkundur ve κ degeri mutlaka γ2 − 2; degerine esit veya bu degerden buyuk olmalidir. κ degeri ile γ2 − 2; degeri esitligi ise ancak ve ancak Bernoulli dagilimi icin dogrudur. Normal dagilimdan cok farkli sekil gostermeyen sinirsiz carpiklik gosteren dagilimlar icin κ degeri γ2 ile 2γ2 arasinda bulunur.
Bu esitsizlik terimin isbat etmek icin once su terimi ele alalim:
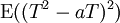 Bunda T = (X − μ)/σ olur. Bu bir karenin matematiksel bekleyisidir. a degeri ne olursa olsun bu non-negatiftir ve ayni zamnda a ifadesinde bir kuadratik denklem olur. Bu da isbati istenilen ifadedir.
Bunda T = (X − μ)/σ olur. Bu bir karenin matematiksel bekleyisidir. a degeri ne olursa olsun bu non-negatiftir ve ayni zamnda a ifadesinde bir kuadratik denklem olur. Bu da isbati istenilen ifadedir.
Kümülantlar
Birinci moment ve ikinci ve ucuncu normalize edilmemis merkezsel momentler dogrusaldirlar; yani eger X ve Y isatistiksel olarak bagimsiz rassal degiskenlerse, o halde
 ve
ve
 ve
ve
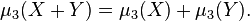 esitlikleri gercektir. (Bu sartlar yalniz bagimsizlik sartina degil daha zayif sartlar altinda bulunan degiskenler icin de gercek olabilri.). Birinci sart her zaman dogru olup ikinci sart da dogru olursa bu degiskenler arasinda korelasyon yoktur.
esitlikleri gercektir. (Bu sartlar yalniz bagimsizlik sartina degil daha zayif sartlar altinda bulunan degiskenler icin de gercek olabilri.). Birinci sart her zaman dogru olup ikinci sart da dogru olursa bu degiskenler arasinda korelasyon yoktur.
Bunun dogrulugunu anlamak icin bu momentlerin ilk uc kumulant olduklaraini ve dorduncu kumulantin ise basiklik katsayisi κ carpi σ4 oldugunu anlamak yeterlidir.
Butun kumulantlar momentlerin polinomlaridir yani [[faktoriyel moment]lerdir. Merkezsel momentler sifir etrafindanki momentlerin polinomlaridir ve bunun aksi de dogrudur.
Örneklem momentleri
Bir anakutle icin momentler bir orneklem k-inci momenti kullanilarak kestirimi yapilabilirler. Orneklem k-inci momenti soyle ifade edilir:
 ve bu anakutleden rasal ornekelem e ile secilmis X1,X2,..., Xn orneklem degerlerine uygulanir.
ve bu anakutleden rasal ornekelem e ile secilmis X1,X2,..., Xn orneklem degerlerine uygulanir.
Bu bir yansiz kestirmdir. Cunku herhangi bir n buyuklukte bir orneklem icin orneklem momentinin matematiksel beklenen degerinin anakutle k-inci momentine esit oldugu hemen gosterilebilir.
 Sıfır değeri etrafında olan momentler en basit olarak bir fonksiyonun momenti diye anılır.
Sıfır değeri etrafında olan momentler en basit olarak bir fonksiyonun momenti diye anılır.Sponsorlu Bağlantılar
Eğer f bir olasılık yoğunluk fonksiyonu ise, o halde yukarıda verilmiş olan entegralin değeri olasılık dağılımınin ninci moment Riemann-Stieltjes entegrali tarafından şöyle verilir:
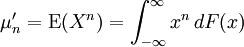
Burada X bu dağılımı gösteren bir rassal değişken ve E bir beklenti operatörüdür.
Eğer
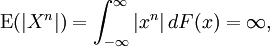
ise momentin mevcut olmadığı kabul edilir. Egğr herhangi bir nokta etrafında ninci moment belirlenebilirse, o halde (n − 1)inci moment de bulunur ve her bir nokta etrafında daha-alt derecelerdeki momentler de bulunur.
Momentlerin Önemi
Sıfır etrafindaki birince moment, eğer anlamlı ise, Xin matematiksel beklentisi yani μ olarak yazilan Xin olasılık dağılımının ortalamasıdır. Daha yüksek dereceler icin merkezsel momentler sıfır etrafında momentlerden daha ilgi çekicidir.
Bir rassal değişken olan Xin olasılık dağılımının ninci merkezsel momenti şudur:
 Böylece birinci merkezsel moment 0 olur.
Böylece birinci merkezsel moment 0 olur.Varyans
İkinci merkezsel moment varyans σ2 olur; bunun pozitif kare kökü standart sapma σ olur.
Normalize edilmiş momentler
Normalize edilmis ninci merkezsel moment veya standardize edilmis moment ninci merkezsel moment bolu σn olur; yani t = (x − μ)/σ ifadesinin ninci momentidir. Bu normalize edilmis momentler boyutsuz niceliklerdir ve herhangi bir dogrusal iskala degisiminden etkilenmeden bir dagilimi temsil edebilirler.
Çarpıklık
Üçüncü merkezsel moment bir dağılımın simetrik olmaması ölçüsüdür. Herhangi bir simetrik dağılım için üçüncü merkezsel moment, eğer tanımlanabilirse, 0 olur. Normalize edilmiş üçüncü merkezsel moment γ ile yazılıp çarpıklık adı ile anılır. Sol tarafa çarpıklık gösteren (yani sol kuyruğu daha ağır basan) bir dağılım negatif çarpıklık gösterir. Sağ tarafa çarpıklık gösteren (yani sağ kuyruğu daha ağır basan) bir dağılım pozitif çarpıklık gösterir.
Normal dağılımdan çok fazla farklı olmayan dağılımlar icin medyan μ − γσ/6 değerine yaklasik olur ve mod ise μ − γσ/2 ifadesine yaklaşıktır.
Basıklık
Dorduncu merkezsel moment dagilimin ince ve sivri mi yoksa kalin ve basik mi oldugunun olcusudur ve bu niteligi ayirt etmek icin ayni varyansi gosteren bir normal dagilim ile karsilastirma yapilir. Dorduncu merkezsel moment, bir dortlu ustelin matematiksel beklentisi oldugu icin, eger tanimi yapilabilirse, (sadece dejenere nokta dagilim haric) her zaman pozitif deger alir. Bir normal dagilim icin dorduncu merkezsel moment 3σ4 olur.
Basıklık olcusu olarak kullanilan basıklık fazlalığı katsayisi κ, normalize edilmis dorduncu merkezsel moment eksi 3 olarak tanimlanir. (Gelecek kisimda gosterildigi gibi, bu olcu dorduncu kümülant bolu varyans kare olarak da tanimlanir.) Bazi otoriteler bu sekilde normal dagilimi koordinatlarin orijinine koymak icin kullanilan eksi 3 terimini tenkit etmektedirler. Eger bir dagilim aortalama degerinde bir doruk ve iki tarafinda uzun kuyruklara gosterirse, dorduncu moment degeri buyuk olur ve basiklik olcusu κ pozitifdir; aksi halde dorduncu moment degeri kucuk ve basiklik olcusu κ negatif olur. Boylece sinirlanmis dagilimlarda basiklik dusuktur.
Basıklık olcusu hic sinirsiz bir sekilde pozitif olmasi mumkundur ve κ degeri mutlaka γ2 − 2; degerine esit veya bu degerden buyuk olmalidir. κ degeri ile γ2 − 2; degeri esitligi ise ancak ve ancak Bernoulli dagilimi icin dogrudur. Normal dagilimdan cok farkli sekil gostermeyen sinirsiz carpiklik gosteren dagilimlar icin κ degeri γ2 ile 2γ2 arasinda bulunur.
Bu esitsizlik terimin isbat etmek icin once su terimi ele alalim:
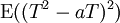 Bunda T = (X − μ)/σ olur. Bu bir karenin matematiksel bekleyisidir. a degeri ne olursa olsun bu non-negatiftir ve ayni zamnda a ifadesinde bir kuadratik denklem olur. Bu da isbati istenilen ifadedir.
Bunda T = (X − μ)/σ olur. Bu bir karenin matematiksel bekleyisidir. a degeri ne olursa olsun bu non-negatiftir ve ayni zamnda a ifadesinde bir kuadratik denklem olur. Bu da isbati istenilen ifadedir.Kümülantlar
Birinci moment ve ikinci ve ucuncu normalize edilmemis merkezsel momentler dogrusaldirlar; yani eger X ve Y isatistiksel olarak bagimsiz rassal degiskenlerse, o halde
 ve
ve ve
ve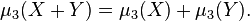 esitlikleri gercektir. (Bu sartlar yalniz bagimsizlik sartina degil daha zayif sartlar altinda bulunan degiskenler icin de gercek olabilri.). Birinci sart her zaman dogru olup ikinci sart da dogru olursa bu degiskenler arasinda korelasyon yoktur.
esitlikleri gercektir. (Bu sartlar yalniz bagimsizlik sartina degil daha zayif sartlar altinda bulunan degiskenler icin de gercek olabilri.). Birinci sart her zaman dogru olup ikinci sart da dogru olursa bu degiskenler arasinda korelasyon yoktur.Bunun dogrulugunu anlamak icin bu momentlerin ilk uc kumulant olduklaraini ve dorduncu kumulantin ise basiklik katsayisi κ carpi σ4 oldugunu anlamak yeterlidir.
Butun kumulantlar momentlerin polinomlaridir yani [[faktoriyel moment]lerdir. Merkezsel momentler sifir etrafindanki momentlerin polinomlaridir ve bunun aksi de dogrudur.
Örneklem momentleri
Bir anakutle icin momentler bir orneklem k-inci momenti kullanilarak kestirimi yapilabilirler. Orneklem k-inci momenti soyle ifade edilir:
 ve bu anakutleden rasal ornekelem e ile secilmis X1,X2,..., Xn orneklem degerlerine uygulanir.
ve bu anakutleden rasal ornekelem e ile secilmis X1,X2,..., Xn orneklem degerlerine uygulanir.Bu bir yansiz kestirmdir. Cunku herhangi bir n buyuklukte bir orneklem icin orneklem momentinin matematiksel beklenen degerinin anakutle k-inci momentine esit oldugu hemen gosterilebilir.
Vikipedi
ѕнσω мυѕт gσ ση ツ

 Matematik Momentleri
Matematik Momentleri
