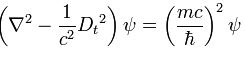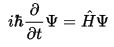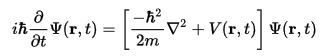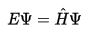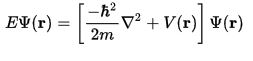Schrödinger denklemi
kuvantum mekaniğinin temel denklemi. AvusturyalI fizikçi Erwin Schrödinger tarafından 1926’da ortaya konan bu denklem, kuvantum mekaniğinde, Newton hareket yasalarının klasik mekanik için taşıdığı temel öneme eşdeğer bir önem taşır.
Temelde bir dalga denklemi olan Schrödinger denklemi, temel parçacıkların hareketlerini yönlendiren olasılık dalgalarını (bir başka deyişle dalga fonksiyonlarını) ve bu dalgaların dış etkiler altındaki değişim biçimlerini betimler. Schrödinger, oluşturduğu denklemi hidrojen atomuna uygulayarak bu atoma ilişkin birçok özelliği olağanüstü bir kesinlikle belirlediğini göstermiştir. Schrödinger denkleminden atom fiziğinde, nükleer fizikte ve katilar fiziğinde yaygın olarak yararlanılır.
Schrödinger denklemi kapalı formda şöyle ifade edilebilir:
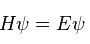
Burada H, Hamiltonyen' i temsil eder. Hamiltonyen, parçacığın toplam enerjisini veren bir operatördür ve
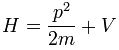
şeklinde ifade edilir. İlk terim kinetik enerjiyi, ikinci terim ise potansiyel enerjiyi temsil eder. Momentum operatörü
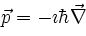
denklemde yerine konursa Schrödinger denkleminin sol tarafı elde edilir.
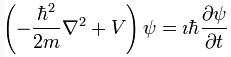
Bu zamana bağlı Schrödinger denklemidir. Denklemin sağ tarafının sıfıra eşit olması durumunda zamandan bağımsız Schrödinger denklemi karşımıza çıkar. Burada
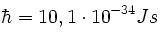
değerinde Planck sabiti, m; parçacığın kütlesi, V; potansiyel enerji,
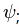
parçacığa eşlik eden dalga fonksiyonudur. Parçacığın kinetik enerjisinin hareket etmezken sahip olduğu iç enerjisinden oldukça büyük olması durumunda enerjisi göreli olarak ifade edileceğinden
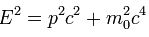
şeklinde olur. Bu sayede elde edilen Schrödinger denklemine, Relativistik (göreli) Schrödinger Denklemi denir ve
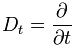
olmak üzere şu formda yazılır.
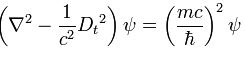
Denklemin çözümü için, parçacığın bulunduğu duruma göre içinde olduğu potansiyeller şöyle özetlenebilir:
V'nin sıfır olması durumunda serbest parçacık durumu incelenir. Sıfırdan farklı durumlarda parçacığın enerjisinin uygulanan potansiyelden büyük veya küçük olması koşullarına göre değişen çözümler bulunur. Parçacığın enerjinisinin uygulanan potansiyelden küçük olması ancak belirli bir genişlikten sonra bu potansiyel engelin kaldırılması durumunda Tünel Etkisi gözlemlenir. Akım yoğunluğu hesaplanarak geçme ve yansıma katsayıları bulunur.
Değişen potansiyellere örnek; basit harmonik titreştirici ve Coulomb potansiyelleridir. Bunlar bir katıdaki atomların titreşimi ve atomdaki çekirdeğe bağlı elektronların hareketini kapsar.
Zaman-bağımlı denklem
Fiziksel durum(durgun durum) üzerindeki Schrödinger denklemi formudur(özel durum için aşağıya bakınız). En iyi genel form zaman-bağımlı Schrödinger denklemidir, bu ise zamanla gelişen sistemin bir tanımını verir:
Denklem-1 Zaman-bağımlı Schrödinger denklemi (genel) 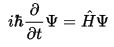
Burada
i sanal birimdir,
ħ 2π ile Planck sabitinin oranıdır ,
"∂/∂t" sembolü bir t zamana gore kısmi türev ile ayırır ,
Ψ kuantum sistemin dalga fonksiyonudur, ve
H Hamiltonyen işlemcidir (herhangi bir dalga fonksiyonu toplam enerjiyi karakterize eder ve duruma bağlı olarak farklı biçimler alır).
En ünlü örneği bir elektrik alanı içinde(ama bir manyetik alan değil; bakınız Pauli denklemi) tek bir parçacık taşıyan göreli olmayan Schrödinger denklemidir :
Bir dalga fonksiyonu bu göreli olmayan Schrödinger denklemi V=0ile tatmin edicidir. Diğer bir değişle, bu boş uzay aracılığıyla bir parçacığın serbestçe seyahatine karşılıktır.Dalga fonksiyonunun buradagerçel kısmı çiziliyor.
Denklem-2 Zaman-bağımlı Schrödinger denklemi (tek ama göreli olmayan parçacık) 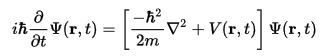
burada m parçacığın kütlesidir, V potansiyel enerjidir, ∇2 Laplasyendir, ve Ψ dalga fonksiyonudur (bu bağlamda daha kesin bir ifadeyle, "konum uzay-dalga fonksiyonu" olarak adlandırılır). Bu daha net bir ifadeyle, "toplam enerji kinetik enerji artı potansiyel enerjiye eşittir", ama şartlar aşağıda açıklanan sebeplerden ötürü bilmediğiniz formlar haline gelir.
Verilen bu bir doğrusal kısmi diferansiyel denklem özel diferansiyel işlemciler içerir. Bu ayrıca bir difüzyon denklemidir, ama aksine ısı denklemi, bu tek ayrıca verilen bir dalga denklemi sanal birim geçici terim içinde mevcuttur.
"Schrödinger denklemi" terimine hem genel denkleminin (ilk yukarıda kutu), hem de belirli bir göreli olmayan sürümün (ikinci yukarıda ve bunun varyasyonları kutu) de başvurabilirsiniz. kuantum mekaniği boyunca kullanılan,genel denklem her şey için,Hamiltoniyen'den çeşitli karmaşık ifadeler takarak Dirac denklemi'nden kuantum alan teorisi'ne kadar gerçekten oldukça geneldir. Özel relativistik sürümü basitleştirilmiş birçok durumda gerçekliğe oldukça doğru yaklaşım, ama diğerleri de çok yanlıştır.(ayrıca görelilik kuantum mekaniği ve görelilik kuantum alan teorisi).
Schrödinger denklemini uygulamak için, Hamilton operatörü daha sonra Schrödinger denklemine yerleştirilir sistemi oluşturan taneciklerin kinetik ve potansiyel enerji için muhasebe sistemi için ayarlanır.Oluşan kısmi diferansiyel denklem sistemi ile ilgili bilgi içeren dalga fonksiyonu, için çözülmüştür.
Zaman-bağımsız denklem
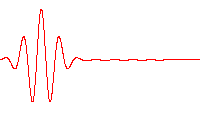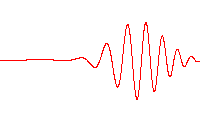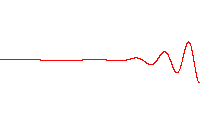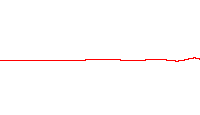
bu her üç satırın bir dalga fonksiyonudır.,bunlar zaman-bağımlı Schrödinger denklemi için uygun bir harmonik titreşimcidir.Sol:dalga fonksiyonunun gerçek kısmı (mavi) ve sanal kısmı (kırmızı). Sağ:Verilen bir konumda bu dalga fonksiyonu ile bulunan parçacığın olasılık dağılımıdır . üst iki satır durağan durumların örnekleridir, bunlar durgun dalgalara karşılıktır. Alt satır bir durumun bir örneğidir bu bir durağan durum değildir. sağ sütunda gösterilen durağan duruma "durağanlık" denir.
zaman-bağımsız Schrödinger denklemi tahmin edilen dalga fonksiyonları durgun dalgalar formu olabilir, adı durağan durumlar (ayrıca "yörüngeler" denir,atomik yörüngeler içinde olarak veya moleküler yörüngeler). eğer durağan durumun üzerinde sınıflandırılmış ve anlaşılıyorsa bu durum burada kendine özgü bir şekilde önemlidir,ve herhangi durum için zaman-bağımlı Schrödinger denklemi çözmeye kolayca alınır .zaman-bağımlı Schrödinger denklemi durağan durum tanıtan denklemdir. (Bu yalnız kullanılıyor ise Hamiltonyenin kendisi zaman üzerinde bağımlı değildir. Genel olarak, dalga fonksiyonuna hala bir bağımlılık vardır! )
Denklem-1 Zaman-bağımsız Schrödinger denklemi (genel) 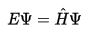
Durum denkleminin sözel ifadesi:
- Belli bir Ψ dalga fonksiyonu üzerinde Hamiltonian operatör hareketleri ise,ve sonuç aynı Ψ dalga fonksiyonuna orantılı , ise Ψ bir durağan durumdur, ve sabit orantılılıktır, E, Ψ durumunun enerjisidir.
Zaman-bağımlı Schrödinger denklemi aşağıda daha fazla tartışıldı. doğrusal cebir terminolojisi içinde, bu denklem bir özdeğer denklemidir.
Daha önce olduğu gibi, göreli-olmayan Schrödinger denklemi için en ünlü bulgu bir tek parçacık bir elektrik alanı içinde taşınır (ama bir manyetik alan değil):
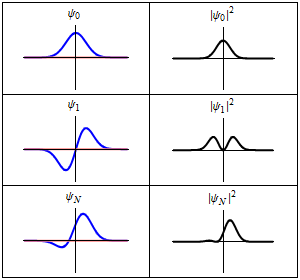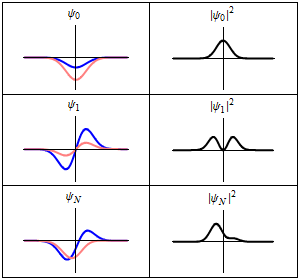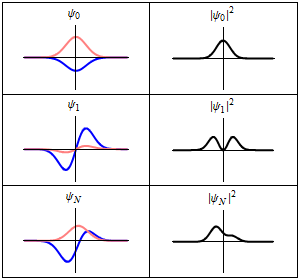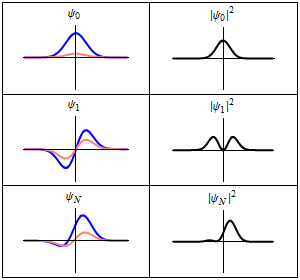
bu her üç satırın bir dalga fonksiyonudır.,bunlar zaman-bağımlı Schrödinger denklemi için uygun bir harmonik titreşimcidir.
- Sol: dalga fonksiyonunun gerçek kısmı (mavi) ve sanal kısmı (kırmızı).
- Sağ: Verilen bir konumda bu dalga fonksiyonu ile bulunan parçacığın olasılık dağılımıdır .
- üst iki satır durağan durumların örnekleridir, bunlar durgun dalgalara karşılıktır.
- Alt satır bir durumun bir örneğidir bu bir durağan durum değildir. sağ sütunda gösterilen durağan duruma "durağanlık" denir.
Denklem-2 Zaman-bağımsız Schrödinger denklemi (tek göreli olmayan parçacık) 

 Schrödinger Denklemi
Schrödinger Denklemi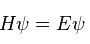 Burada H, Hamiltonyen' i temsil eder. Hamiltonyen, parçacığın toplam enerjisini veren bir operatördür ve
Burada H, Hamiltonyen' i temsil eder. Hamiltonyen, parçacığın toplam enerjisini veren bir operatördür ve 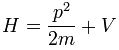 şeklinde ifade edilir. İlk terim kinetik enerjiyi, ikinci terim ise potansiyel enerjiyi temsil eder. Momentum operatörü
şeklinde ifade edilir. İlk terim kinetik enerjiyi, ikinci terim ise potansiyel enerjiyi temsil eder. Momentum operatörü 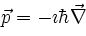 denklemde yerine konursa Schrödinger denkleminin sol tarafı elde edilir.
denklemde yerine konursa Schrödinger denkleminin sol tarafı elde edilir.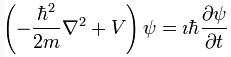
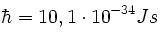 değerinde Planck sabiti, m; parçacığın kütlesi, V; potansiyel enerji,
değerinde Planck sabiti, m; parçacığın kütlesi, V; potansiyel enerji, 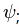 parçacığa eşlik eden dalga fonksiyonudur. Parçacığın kinetik enerjisinin hareket etmezken sahip olduğu iç enerjisinden oldukça büyük olması durumunda enerjisi göreli olarak ifade edileceğinden
parçacığa eşlik eden dalga fonksiyonudur. Parçacığın kinetik enerjisinin hareket etmezken sahip olduğu iç enerjisinden oldukça büyük olması durumunda enerjisi göreli olarak ifade edileceğinden 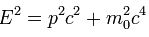 şeklinde olur. Bu sayede elde edilen Schrödinger denklemine, Relativistik (göreli) Schrödinger Denklemi denir ve
şeklinde olur. Bu sayede elde edilen Schrödinger denklemine, Relativistik (göreli) Schrödinger Denklemi denir ve 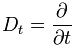 olmak üzere şu formda yazılır.
olmak üzere şu formda yazılır.