Ziyaretçi
Aritmetik Ortalama
İstatistik bilim dalında hem betimsel istatistik alanında hem de çıkarımsal istatistik alanında en çok kullanan merkezsel konum ölçüsü aritmetik ortalamadır. Genel olarak aritmetik ortalama pratik veya teorik tüm veri dizisinin toplanmasi ve bu toplamin veri sayısına bölünmesi ile elde edilen bir sayıdır.
Tanımlama
Matematiksel biçimde aritmetik ortalama anakütle için μ ve örneklem için (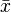 ) olarak ifade edilir.
) olarak ifade edilir.
Genel formül
Anakütle büyüklüğü N ve örneklem büyüklüğü n olduğu kabul edilirse, aritmetik ortalama hesaplaması için formüller şöyle verilir: Anakütle aritmetik ortalaması:

Örneklem aritmetik ortalaması:
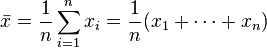
Örnegin, bir sınıftaki farklı kişilerin aldığı not veya sayının toplamının kişi sayısına bölünmesi aritmetik ortalamayı verir.
Çokluk dağılım verileri için formül
Bazan veriler daha önceden özetlenip sınıflara ayrılıp gruplanmışlardır. Bu gruplanmış veri özetine çokluk dağılımı adı verilmektedir. Bu halde N veya n sayıda veri dizisi m sayıda gruba ayrılmakta ve her grup belli bir minimum ve maksimum değerler arasında bulunan verileri kapsamaktadır. Böylece veriler bir çokluk tablosu veya frekans tablosu içinde m sayıda sınıf birinci sütunda ve her sınıf içinde bulunan çokluk (frekans) ( için fj)) ikinci sütunda yer almaktadır. Bu tür özetlenmiş veri dizisi için bir yaklaşık aritmetik ortalama bulunabilir. Bu yaklaşık bir değerdir çünkü her veri için gerçek x değeri değil, ancak sınıfsal ortalama (
için fj)) ikinci sütunda yer almaktadır. Bu tür özetlenmiş veri dizisi için bir yaklaşık aritmetik ortalama bulunabilir. Bu yaklaşık bir değerdir çünkü her veri için gerçek x değeri değil, ancak sınıfsal ortalama ( için
için  ) kullanılmaktadır. Böylece çokluk dağılımlarında aritmetik ortalama hesaplanırken şu formüller kullanılır:
) kullanılmaktadır. Böylece çokluk dağılımlarında aritmetik ortalama hesaplanırken şu formüller kullanılır:
Anakütle ortalaması:

Örneklem ortalamasi

Dezavantajları
Aritmetik ortalama çok popüler olarak hesaplanıp kullanılmakla beraber bazı önemli dezavantajları bulunmaktadır.
Sponsorlu Bağlantılar
Tanımlama
Matematiksel biçimde aritmetik ortalama anakütle için μ ve örneklem için (
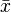 ) olarak ifade edilir.
) olarak ifade edilir.Genel formül
Anakütle büyüklüğü N ve örneklem büyüklüğü n olduğu kabul edilirse, aritmetik ortalama hesaplaması için formüller şöyle verilir: Anakütle aritmetik ortalaması:

Örneklem aritmetik ortalaması:
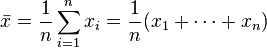
Örnegin, bir sınıftaki farklı kişilerin aldığı not veya sayının toplamının kişi sayısına bölünmesi aritmetik ortalamayı verir.
Çokluk dağılım verileri için formül
Bazan veriler daha önceden özetlenip sınıflara ayrılıp gruplanmışlardır. Bu gruplanmış veri özetine çokluk dağılımı adı verilmektedir. Bu halde N veya n sayıda veri dizisi m sayıda gruba ayrılmakta ve her grup belli bir minimum ve maksimum değerler arasında bulunan verileri kapsamaktadır. Böylece veriler bir çokluk tablosu veya frekans tablosu içinde m sayıda sınıf birinci sütunda ve her sınıf içinde bulunan çokluk (frekans) (
 için fj)) ikinci sütunda yer almaktadır. Bu tür özetlenmiş veri dizisi için bir yaklaşık aritmetik ortalama bulunabilir. Bu yaklaşık bir değerdir çünkü her veri için gerçek x değeri değil, ancak sınıfsal ortalama (
için fj)) ikinci sütunda yer almaktadır. Bu tür özetlenmiş veri dizisi için bir yaklaşık aritmetik ortalama bulunabilir. Bu yaklaşık bir değerdir çünkü her veri için gerçek x değeri değil, ancak sınıfsal ortalama ( için
için  ) kullanılmaktadır. Böylece çokluk dağılımlarında aritmetik ortalama hesaplanırken şu formüller kullanılır:
) kullanılmaktadır. Böylece çokluk dağılımlarında aritmetik ortalama hesaplanırken şu formüller kullanılır:Anakütle ortalaması:

Örneklem ortalamasi

Dezavantajları
Aritmetik ortalama çok popüler olarak hesaplanıp kullanılmakla beraber bazı önemli dezavantajları bulunmaktadır.
- Aşırı değerlere duyarlı (yani güçsüz) bir merkezsel konum ölçüsüdür. Eğer veri dizisi için asimetrik olarak sadece bir uçsal değer ya aşırı küçük ya aşırı büyük ise aritmetik ortalama o aşırı değere yaklaşma gösterir.
- Aritmetik ortalama her türlü ölçülme ölçekli sayısal veri için kullanılamaz. İsimsel ölçekli sayısal veriler için aritmetik ortalama anlamsızdır. Sırasal ölçekli sayısal veriler için aritmetik ortalama kullanılması büyük tartışmalara açıktır. Birçok kişi değişik kişilerin sıralamalarının aynı olduğunu kabul etmedikleri için elde edilen verilerin toplamının ve bu toplamdan çıkartılan aritmetik ortalamanın anlamsız olacağını kabul etmektedirler. Ancak işletme alanı, davranışsal bilimler ve sosyal bilimlerde, özellikle anket verileri, sırasal ölçekli olmakta, ve buna rağmen bu verilerin aritmetik ortalamaları pratikte onemli alanlarda kullanılmaktadır. Aralıksal ölçekli ve oransal ölçekli sayısal veriler için aritmetik ortalama anlamlıdır.

 Aritmetik Ortalama
Aritmetik Ortalama
