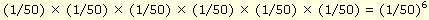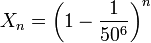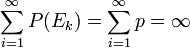Sonsuz Maymun Kuramı
VIP VIP Üye
Sonsuz Maymun Kuramı
Vikipedi, özgür ansiklopedi
Sonsuz maymun kuramı, bir daktilonun tuşlarına gelişigüzel dokunan bir maymunun belirli bir metni (örneğin William Shakespeare'in tüm yapıtları) sonsuz zaman dilimi içinde yazabileceğini ortaya koyan matematik kuramıdır.
Burada "neredeyse kesin" söz öbeği matematiksel bir terim olarak öne çıkmaktadır. Kuramda geçen "maymun" sözcüğü ise, gerçek bir maymun yerine sonsuz harften oluşan bir rastgele dizi üreten aygıt anlamına gelmektedir. Kuram, sonsuzluk kavramına ilişkin akıl yürütmelerin konu olduğu tehlikeyi ortaya koymaktadır. Bir maymunun Shakespeare'in "Hamlet" adlı yapıtı gibi çalışmaları tümüyle aynı biçimde yazabilme olasılığı o denli küçüktür ki, bu durumun evrenin yaşı ölçeğinde gerçekleşme şansı önemsizdir; ancak, kesinlikle sıfır değildir.
Kuramın çok ya da sonsuz sayıda yazıcı içerdiği uyarlamaları olduğu gibi hedef metnin büyüklüğü bir dizi ile kütüphane arasında değişebilmektedir. Kuramın kökleri Aristoteles'in "Oluş ve Bozuluş Üzerine" ve Cicero'nun "De natura deorum" adlı yapıtlarıyla Blaise Pascal ve Jonathan Swift'in düşüncelerine dayanmaktadır. Émile Borel ve Arthur Eddington 20. yüzyılda kuramı, istatistiksel mekaniğin gizli zaman cetvelini ortaya koymak amacıyla kullanmışlardır. Birçok Hıristiyan savunucu ve Richard Dawkins, evrim için kullanılan maymun benzetmesinin uygunluğu konusunda farklı görüşler ileri sürmüşlerdir.
Yazı yazan maymunlara olan popüler ilgi yazın, televizyon, radyo, müzik ve İnternet'teki birçok örnekte görülebilmektedir. 2003 yılında altı sorguçlu kara şebekle (Macaca nigra) bir deney gerçekleştirilmiştir ancak ortaya konan yazınsal katkı, 'S' harfinin çoğunlukta olduğu beş sayfalık bir belgedir.
Çözüm
Kanıt
Kuramın oldukça anlaşılabilir bir kanıtı bulunmaktadır. İki olay istatistiksel olarak bağımsızsa (olaylar birbirinin sonucunu etkilemiyorsa) bu iki olayın birlikte gerçekleşme olasılığı bu olayların ayrı ayrı gerçekleşme olasılıklarının çarpımına eşittir.
Örneğin, Sidney'in yağmurlu bir gün geçirme olasılığı 0.3 ve San Francisco'da o gün bir deprem olma olasılığı 0.008 ise bu iki olayın birlikte gerçekleşme olasılığı 0.3 × 0.008 = 0.0024'e eşit olacaktır.
Daktilonun 50 tuştan oluştuğu ve yazılacak sözcüğün "maymun" olduğu varsayılsın. Tuşlara rastgele basıldığı göz önüne alınırsa yazılan ilk harfin m olma olasılığı 1/50'dir. Benzer biçimde, ikinci harfin a olma olasılığı da 1/50'ye eşit olacaktır. Art arda yazılan harfler birbirinden bağımsız olaylar oluşturduğundan ilk altı harfin "maymun" sözcüğünü oluşturma olasılığı,
n arttıkça Xn azalmaktadır:
Bu görüş, sonsuz sayıda maymunun en az birinin metni, daktiloyu neredeyse hatasız kullanan bir insanla aynı sürede yazabildiğini göstermektedir. Bu durumda,
Ne var ki, fiziksel bakımdan anlamlı sayıda maymunun fiziksel bakımdan anlamlı bir süre boyunca yazma denemesi yaptığı düşünülürse sonuç, yukarıda elde edilenin tam tersidir. Maymun sayısı gözlemlenebilir evrendeki parçacık sayısına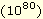
eşitse ve her maymun evrenin yaşının 
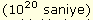100 katı süre boyunca saniyede 1000 harf yazabiliyorsa elde edilen metnin kısa bir kitabın bile birebir aynısı olma olasılığı sıfıra yakındır.
Sonsuz Diziler
Yukarıda açıklanan sonuçlar diziler yardımıyla daha genel ve akıcı bir biçimde ifade edilebilmektedir.
İlk kuram da buna benzer biçimde kanıtlanabilmektedir. Rastgele dizi çakışmayan bölmelere ayrılır ve Ek, k. bölmenin hedef diziye eşit olması olayı olarak tanımlanırsa istenilen sonuç elde edilir.
Olasılıklar
Noktalama imleri, boşluk ve büyük-küçük harf kullanımı göz ardı edilirse bir maymunun Hamlet'in ilk harfini doğru yazma olasılığı 26'da 1, ilk iki harfini doğru yazma olasılığı,
Yaklaşık 130.000 karakterden oluşan "Hamlet"i ilk denemede doğru yazma olasılığı,
Geçmiş
İstatistiksel Mekanik
"Daktilografik" (yazıcı) maymunları (Fransızca: singes dactylographes, Fransızca singe sözcüğü maymun ve insansıları kapsamaktadır) temel alan kuram biçimi Émile Borel'in 1913 yılında yazdığı "Mécanique Statistique et Irréversibilité" (İstatistiksel mekanik ve tersinmezlik) adlı makalesi ve 1914'te yayımlanan "Le Hasard" adlı kitabında yer almaktadır. Burada kullanılan "maymunlar" gerçek varlıkları temsil etmekten çok büyük bir rastgele harf dizisi oluşturabilmek için kullanılan imgesel bir yöntemi belirtmektedir. Borel'e göre, bir milyon maymunun günde on saat boyunca yazı yazması durumunda bile dünyanın en varsıl kütüphanesinde bulunan kitapların birebir kopyalanması neredeyse olanaksızdır.
Arthur Eddington, "The Nature of the Physical World" (1928) adlı kitabında Borel'i şöyle desteklemiştir:
Temeller ve "Toplam Kütüphane"
Arjantinli yazar Jorge Luis Borges 1939 yılında yazdığı "The Total Library" adlı makalesinde sonsuz maymun kavramını Aristoteles'in Metafizik adlı yapıtıyla temellendirmektedir. Dünyanın atomların rastgele konumlanmalarından doğduğunu düşünen Lefkippos'un görüşlerini genişleten Aristoteles, atomların türdeş olduklarını ve oluşturdukları birleşimin yalnızca biçim, konum ve sıralamaya bağlı değiştiğini vurgulamaktadır. Yunan filozof bu durumu "De Generatione et Corruptione" (Oluş ve Bozuluş Üzerine) adlı yapıtında trajedi ile komedi arasındaki ilişkiyle özdeşleştirmektedir. Cicero'nun üç yüzyıl sonra yayımladığı "De natura deorum" (Tanrıların Doğası) bu atomcu görüşe karşı çıkmaktadır:
Uygulamalar ve Eleştiriler
Evrim
Başlangıçtaki karışıklığa karşın maymun ve daktilo görüşleri günümüzde evrim üzerinde yapılan tartışmalarda aynı biçimde ifade edilmektedir. Örneğin, bir Hıristiyan savunucu olarak öne çıkan Doug Powell, bir maymunun "Hamlet"i şans eseri yazmış olsa bile bu yapıtı üretmiş olamayacağını, bunun nedeninin ise maymunun iletişim becerisine sahip olmaması olduğunu öne sürmüştür. Düşünürün doğal yasaların DNA bünyesinde saklanan bilgiyi üretemeyeceğine ilişkin savı da buna koşut bir görüş olarak değerlendirilmektedir. Daha yaygın biçimde seslendirilen görüş ise Aziz John F. MacArthur'un bir amibi tenyaya dönüştürmek için gerekli mutasyonların oluşma olasılığının bir maymunun Hamlet'in kendi kendine yaptığı konuşmaları yazma olasılığı kadar düşük olduğuna ilişkin savıdır. Buna göre, herhangi bir yaşam türü için ortaya atılan evrim iddialarının hiçbir geçerliliği yoktur.
Evrimsel biyolog Richard Dawkins yazı yazan maymun kavramını 1986'da yayımlanan Kör Saatçi adlı kitabında işlemiş ve doğal seçilimin gelişigüzel mutasyonlarla biyolojik çeşitlilik oluşturma yeteneğini göstermeye çalışmıştır. Dawkins kendi ürettiği samur programını kullanarak Hamlet metninde geçen "METHINKS IT IS LIKE A WEASEL" tümcesini oluşturmayı başarmıştır. Rastgele seçtiği bir atadan türeyen kuşakları "besleyip" atayla birebir aynı soyları seçen Dawkins rastgele mutasyonlar yaratabilmiştir. Rastgele seçimler ham bilgi üretirken art arda sıralanan tüm seçimler asıl bilgiyi açığa çıkarmaktadır.
Evrim ve sınır tanımaksızın yazı yazmasına izin verilen maymun arasında kurulan ilişkiyi geri çevirmenin bir diğer yolu ise maymunun karakterleri tek tek ve birbirinden bağımsız biçimde yazması olgusu içinde gizlidir. Biyolojik evrimden çok düşünce evrimine odaklanan Hugh Petrie daha karmaşık bir kuruluma gerek olduğunu savunmaktadır:
Yazın Kuramı
R. G. Collingwood 1938'de sanatın şans eseri üretilemeyeceğini öne sürmüş ve eleştirilerini iğneleyici bir biçimde dile getirmiştir.
Jorge J. E. Gracia elde edilen metinlerin birebir aynı oluşunun bir yazar sorunu oluşturduğunu düşünmektedir. Herhangi bir anlamlandırma amacı gütmeyen bir maymun "Hamlet" ölçeğinde bir yapıtı birebir yazabiliyorsa metinlerin yazarlara olan gereksinimi ortadan kalkacaktır. Olası çözümler, metni bulan ve onu "Hamlet" olarak adlandıranın yazar olduğu ya da Shakespeare'in yazar, maymunun yardımcı, metni bulanın ise okuyucu olduğu görüşünü benimsemektir. Ne var ki, bu çözümlerin bazı sorunları bulunmaktadır. Maymunun yapıtı Shakespeare doğmadan önce yazmış olması, Shakespeare'in hiç doğmamış olması ya da maymunun ürettiği metnin hiçbir zaman bulunmamış olması durumları olası sorunlardandır.
Rastgele Sayı Üretimi
Kuram, zaman ve kaynak tüketimi bakımından uygulanması olanaksız olan bir düşünce deneyini konu edinmektedir. Buna karşın, kuramın rastgele metin üretimindeki yeri tartışmasızdır.
The New Yorker'da yer alan bir yazıya göre Scottsdale, Arizonalı bir araştırmacı olan Dan Oliver tarafından çalıştırılan bir bilgisayar programı 4 Ağustos 2004 tarihinde sonuç vermiştir. 42.162.500.000 milyar milyar maymun yılı boyunca çalışan deney öbeği içinde yer alan bir maymun,
"Maymun Shakespeare Simülatörü" adıyla 1 Temmuz 2003 tarihinde açılan web sitesi rastgele metinler üreten büyük bir maymun topluluğunu taklit eden bir Java uygulaması içermektedir. Uygulamanın amacı maymunların Shakespeare'in herhangi bir yapıtını ne kadar sürede yazabileceklerini ortaya çıkarmaktır. Örneğin, uygulamanın "IV. Henry, 2. Bölüm" adlı oyunda yer alan şu satırı üretmesi "2.737.850 milyon milyar milyar milyar maymun yılı" sürmüştür:
İdeal bir maymunun belirli dizileri hangi sıklıkla yazması gerektiğini ele alan istatistiklere ilişkin sorular rastgele sayı üreteçleri için yapılan uygulamalı deneyleri de tetikleyebilmektedir. En basitten "oldukça karmaşığa" dek uzanan bu deneyler berimsel bilimler profesörleri George Marsaglia ve Arif Zaman'a göre "çakışan mli testler" olarak adlandırılmaktadır. Ne var ki, bunlsrın "maymun testleri" olarak adlandırılmasının öğrencilerin konuya olan ilgilerini artırdığı düşünülmektedir. Adı geçen biliminsanlarının farklı test sınıfları ve sonuçlarına ilişkin 1993'te yayımladıkları bir raporları bulunmaktadır.
Gerçek Maymunlar
Primat davranışçıları Cheney ve Seyfarth gerçek maymunların Romeo ve Juliet adlı yapıtı yazabilmeleri için şansa gerek duyduklarını belirtmektedir. İnsansılar ve şempanzelerden farklı olarak maymunlar bir zihin kuramına sahip olmamakta ve kendi bilgi, duygu ve inançlarıyla başkalarınınkiler arasında bir ayrım yapamamaktadırlar. Bir maymun oyun yazmayı öğrense ve kurguladığı karakterlerin davranışlarını tanımlayabilse bile bu karakterlerin zihinlerini açığa çıkaramayacağı için ortaya konan yapıt alaycı bir trajedi olacaktır.
Plymouth Üniversitesi öğretim üyeleri ve öğrencilerinden oluşan bir çalışma öbeği 2003 yılında gerçek maymunların yazınsal üretimini araştırmak üzere Sanat Kurulu'ndan 2000 sterlinlik bir ödenek almıştır. Araştırmacılar Devon, İngiltere'deki Paignton Hayvanat Bahçesi'nde bulunan altı sorguçlu kara şebeğin önüne bir klavye bırakmış ve sonuçları bir web sitesi üzerinde yayınlayabilmek için bir radyo bağlantısı kurmuşlardır. Takım üyelerinden Mike Phillips bu deneyimi "heyecan verici ve muhteşem bir şölen" olarak değerlendirmektedir.
Maymunlar, çoğunluğu S harfinden oluşan ve yalnızca beş sayfa uzunluğunda bir üretim yapmakla kalmamış, baba maymun klavyeyi bir taşla ezmeye çalışırken diğer maymunlar çiş ve kakalarını klavye üzerine yapmaktan çekinmemişlerdir. Hayvanat bahçesi fen müdürü bu deneyin "bilimsel geçerliliğinin olmadığını ve yalnızca 'sonsuz maymun' kuramının hatalı olduğunu gösterdiğini" belirtmiştir. Philips, sanat camiası tarafından desteklenen bu projenin temelde bir gösteri sanatı olduğunu ve bundan çok şey öğrendiklerini söylemiştir. Araştırmacı sözlerini şöyle sürdürmüştür:
Sonsuz maymun kuramı ve oluşturduğu imge olasılığın matematiğinin popüler ve ünlü bir ifadesi olarak kabul edilmektedir. Kavramın kamuoyunca tanınmasını sağlayan temel etken sınıf yerine popüler kültür aracılığıyla yayılmasıdır.
Kurama Douglas Adams'ın "Otostopçunun Galaksi Rehberi" adlı romanında bir şaka olarak değinilmiştir.
İlk kez 11.03.1993 tarihinde yayınlanan Amerikan çizgi dizisi "The Simpsons"ın "Last Exit to Springfield" adlı bölümünde Bay Burns şöyle konuşmaktadır:
Çizer Ruben Bolling düşünce deneyini "Tom the Dancing Bug" adlı çizgi filmde bir maymuna söylettiği şu sözlerle taşlamıştır:
Vikipedi, özgür ansiklopedi
Sponsorlu Bağlantılar
Tuşlara gelişigüzel biçimde dokunan bir şempanze yeterli süre verildiğinde Shakespeare'in oyunlarından birini neredeyse kesin olarak yazabilir.
Sonsuz maymun kuramı, bir daktilonun tuşlarına gelişigüzel dokunan bir maymunun belirli bir metni (örneğin William Shakespeare'in tüm yapıtları) sonsuz zaman dilimi içinde yazabileceğini ortaya koyan matematik kuramıdır.
Burada "neredeyse kesin" söz öbeği matematiksel bir terim olarak öne çıkmaktadır. Kuramda geçen "maymun" sözcüğü ise, gerçek bir maymun yerine sonsuz harften oluşan bir rastgele dizi üreten aygıt anlamına gelmektedir. Kuram, sonsuzluk kavramına ilişkin akıl yürütmelerin konu olduğu tehlikeyi ortaya koymaktadır. Bir maymunun Shakespeare'in "Hamlet" adlı yapıtı gibi çalışmaları tümüyle aynı biçimde yazabilme olasılığı o denli küçüktür ki, bu durumun evrenin yaşı ölçeğinde gerçekleşme şansı önemsizdir; ancak, kesinlikle sıfır değildir.
Kuramın çok ya da sonsuz sayıda yazıcı içerdiği uyarlamaları olduğu gibi hedef metnin büyüklüğü bir dizi ile kütüphane arasında değişebilmektedir. Kuramın kökleri Aristoteles'in "Oluş ve Bozuluş Üzerine" ve Cicero'nun "De natura deorum" adlı yapıtlarıyla Blaise Pascal ve Jonathan Swift'in düşüncelerine dayanmaktadır. Émile Borel ve Arthur Eddington 20. yüzyılda kuramı, istatistiksel mekaniğin gizli zaman cetvelini ortaya koymak amacıyla kullanmışlardır. Birçok Hıristiyan savunucu ve Richard Dawkins, evrim için kullanılan maymun benzetmesinin uygunluğu konusunda farklı görüşler ileri sürmüşlerdir.
Yazı yazan maymunlara olan popüler ilgi yazın, televizyon, radyo, müzik ve İnternet'teki birçok örnekte görülebilmektedir. 2003 yılında altı sorguçlu kara şebekle (Macaca nigra) bir deney gerçekleştirilmiştir ancak ortaya konan yazınsal katkı, 'S' harfinin çoğunlukta olduğu beş sayfalık bir belgedir.
Çözüm
Kanıt
Kuramın oldukça anlaşılabilir bir kanıtı bulunmaktadır. İki olay istatistiksel olarak bağımsızsa (olaylar birbirinin sonucunu etkilemiyorsa) bu iki olayın birlikte gerçekleşme olasılığı bu olayların ayrı ayrı gerçekleşme olasılıklarının çarpımına eşittir.
Örneğin, Sidney'in yağmurlu bir gün geçirme olasılığı 0.3 ve San Francisco'da o gün bir deprem olma olasılığı 0.008 ise bu iki olayın birlikte gerçekleşme olasılığı 0.3 × 0.008 = 0.0024'e eşit olacaktır.
Daktilonun 50 tuştan oluştuğu ve yazılacak sözcüğün "maymun" olduğu varsayılsın. Tuşlara rastgele basıldığı göz önüne alınırsa yazılan ilk harfin m olma olasılığı 1/50'dir. Benzer biçimde, ikinci harfin a olma olasılığı da 1/50'ye eşit olacaktır. Art arda yazılan harfler birbirinden bağımsız olaylar oluşturduğundan ilk altı harfin "maymun" sözcüğünü oluşturma olasılığı,
olarak hesaplanır. Bu sayı 15 milyarda birden küçüktür. Bundan sonra yazılacak 6 harfin "maymun" sözcüğünü oluşturması olasılığı aynı nedenle
Yukarıdaki akıl yürütmeye göre "maymun" sözcüğünün oluşmama olasılığı'ya eşit olacaktır.
1 −Yazı denemeleri bağımsız olaylar olduğundan ilk n denemede "maymun" sözcüğünün oluşmama olasılığı
olur.
n arttıkça Xn azalmaktadır:
- n bir milyonken Xn 0.9999 ("maymun" sözcüğünün oluşmama olasılığı yakşalık %99.99),
- n 10 milyarken Xn 0.53 ("maymun" sözcüğünün oluşmama olasılığı yaklaşık %53),
- n 100 milyarken Xn 0.0017 ("maymun" sözcüğünün oluşmama olasılığı yaklaşık %0.17) değerini almaktadır.
- n sonsuza yaklaştıkça Xn sıfıra yaklaşmaktadır.
Bu görüş, sonsuz sayıda maymunun en az birinin metni, daktiloyu neredeyse hatasız kullanan bir insanla aynı sürede yazabildiğini göstermektedir. Bu durumda,
eşitliği sağlanmaktadır. Bu ifadede Xn ilk n maymundan hiçbirinin "maymun" sözcüğünü ilk denemede yazamama olasılığını belirtmektedir. Bu olasılık 100 milyar maymun için %0.17'ye düşmekte, n arttıkça Xn azalmakta ve limit değeri olan sıfıra yaklaşmaktadır.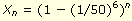
Ne var ki, fiziksel bakımdan anlamlı sayıda maymunun fiziksel bakımdan anlamlı bir süre boyunca yazma denemesi yaptığı düşünülürse sonuç, yukarıda elde edilenin tam tersidir. Maymun sayısı gözlemlenebilir evrendeki parçacık sayısına
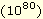eşitse ve her maymun evrenin yaşının 100 katı süre boyunca saniyede 1000 harf yazabiliyorsa elde edilen metnin kısa bir kitabın bile birebir aynısı olma olasılığı sıfıra yakındır.Sonsuz Diziler
Yukarıda açıklanan sonuçlar diziler yardımıyla daha genel ve akıcı bir biçimde ifade edilebilmektedir.
- Karakterlerin tekdüze dağıldığı bir sonsuz dizi içinde herhangi bir sonlu diziyle karşılaşma olasılığı çok yüksektir (dizi birden çok sayıda da bulunabilmektedir).
- Karakterleri rastgele dağılmış sonsuz dizilerin oluşturduğu küme tanımlı olmak üzere, bu küme içinden seçilen herhangi bir sonlu dizi bu kümede yer alan başka bir dizinin öneki olarak bulunmaktadır.
eşitliği elde edilir. Bunun nedeni, olayın sıfırdan farklı bir p gerçekleşme olasılığına sahip olması ve Ek'ların bağımsız oluşlarıdır. Sonsuz sayıda Ek'nın gerçekleşme olasılığı 1'dir.
İlk kuram da buna benzer biçimde kanıtlanabilmektedir. Rastgele dizi çakışmayan bölmelere ayrılır ve Ek, k. bölmenin hedef diziye eşit olması olayı olarak tanımlanırsa istenilen sonuç elde edilir.
Olasılıklar
Noktalama imleri, boşluk ve büyük-küçük harf kullanımı göz ardı edilirse bir maymunun Hamlet'in ilk harfini doğru yazma olasılığı 26'da 1, ilk iki harfini doğru yazma olasılığı,
676'da (26 × 26) 1'dir.Olasılığın üstel büyümesi ilk 20 harfin doğru yazılma olasılığını
düşürmektedir. "Hamlet"in tümü düşünüldüğünde olasılıklar o denli azalmaktadır ki bu değerleri sıfırdan ayırabilmek oldukça güçleşmektedir.1'e
Yaklaşık 130.000 karakterden oluşan "Hamlet"i ilk denemede doğru yazma olasılığı,
Doğru metnin ortaya çıkması için gerekli ortalama harf sayısı da,'da 1'dir.
Noktalama imleri göz önüne alındığında bu sayı,
Tüm evren sonsuz bir süre boyunca yazan maymunlarla doldurulsa bile "Hamlet" adlı yapıtın ortaya çıkma olasılığı,'e çıkmaktadır.
Kittel ve Kroemer'ın deyişiyle "Hamlet"i yazma olasılığı bir olayın uygulanabilirliği bağlamında sıfırdır" ve maymunların bu işi eninde sonunda başaracaklarına ilişkin ifade "çok büyük sayılar hakkında yanlış sonuçlara varılmasına yol açmaktadır."'den düşük olacaktır.
Geçmiş
İstatistiksel Mekanik
"Daktilografik" (yazıcı) maymunları (Fransızca: singes dactylographes, Fransızca singe sözcüğü maymun ve insansıları kapsamaktadır) temel alan kuram biçimi Émile Borel'in 1913 yılında yazdığı "Mécanique Statistique et Irréversibilité" (İstatistiksel mekanik ve tersinmezlik) adlı makalesi ve 1914'te yayımlanan "Le Hasard" adlı kitabında yer almaktadır. Burada kullanılan "maymunlar" gerçek varlıkları temsil etmekten çok büyük bir rastgele harf dizisi oluşturabilmek için kullanılan imgesel bir yöntemi belirtmektedir. Borel'e göre, bir milyon maymunun günde on saat boyunca yazı yazması durumunda bile dünyanın en varsıl kütüphanesinde bulunan kitapların birebir kopyalanması neredeyse olanaksızdır.
Arthur Eddington, "The Nature of the Physical World" (1928) adlı kitabında Borel'i şöyle desteklemiştir:
"Parmaklarımı bir daktilonun tuşları üzerinde gezdirsem ürettiğim uzun sözcük dizisi anlaşılabilir bir tümce oluşturabilir. Bir maymun ordusu daktilolara yüklense British Museum'daki tüm kitapları yazabilirler. Bu olasılık bir kap içerisindeki moleküllerin bir yanda toplanması olasılığından kesinlikle yüksektir."Bu yorumlar çok büyük olmasına karşın sonlu sayıdaki maymunun önemli bir iş üretmesinin inanılmaz derecede düşük olasılığının belirli fiziksel olayların gerçekleşme olasılıklarıyla karşılaştırılmasını gündeme taşımaktadır. Maymunların başarılı denemesinden daha az olası fiziksel olayların uygulamada olanaksız olduğu kesinlikle söylenebilir.
Temeller ve "Toplam Kütüphane"
Arjantinli yazar Jorge Luis Borges 1939 yılında yazdığı "The Total Library" adlı makalesinde sonsuz maymun kavramını Aristoteles'in Metafizik adlı yapıtıyla temellendirmektedir. Dünyanın atomların rastgele konumlanmalarından doğduğunu düşünen Lefkippos'un görüşlerini genişleten Aristoteles, atomların türdeş olduklarını ve oluşturdukları birleşimin yalnızca biçim, konum ve sıralamaya bağlı değiştiğini vurgulamaktadır. Yunan filozof bu durumu "De Generatione et Corruptione" (Oluş ve Bozuluş Üzerine) adlı yapıtında trajedi ile komedi arasındaki ilişkiyle özdeşleştirmektedir. Cicero'nun üç yüzyıl sonra yayımladığı "De natura deorum" (Tanrıların Doğası) bu atomcu görüşe karşı çıkmaktadır:
"Bu görüşü savunan biri şunu da kabul etmek zorunda kalacaktır: Altından ya da herhangi bir maddeden yapılmış çok sayıda harf ortaya dökülürse bu harfler öyle bir dizilişe sahip olabilirler ki Ennius'un yıllıkları ile birebir eşlenebilirler. Şansın bu dizelerin birini bile oluşturabilmesi düşüncesine kuşkuyla bakarım."Borges bu görüşü Blaise Pascal ve Jonathan Swift'te de izlemiş ve yaşadığı dönemde kullanılan ifade biçiminin değiştiğini gözlemlemiştir. 1939 yılına değin egemen düşünce "tümü daktiloya sahip yarım düzine maymunun British Museum'daki tüm kitapları birkaç sonsuzluk zaman diliminde yazabilecekleriydi." (Borges, "bir ölümsüz maymunun bu iş için yeterli olacağını" eklemiştir.) Bunun ardından Borges böyle bir oluşumun sınır tanımaksızın çaba harcaması durumunda meydana getirilebilecek kütüphanenin içeriğini düşlemeye başlamıştır:
"Bu kütüphanede her şey yer alırdı. Her şey... Geleceğin ayrıntılı geçmişi, Eshilos'un "Mısırlılar" adlı oyunu, Ganj sularının şahin uçuşunu yansıtma sayısı, Roma'nın gizli ve gerçek doğası, Novalis adlı ansiklopedi projesinin tam sürümü, 14 Ağustos 1934 şafağında gördüğüm düşler, Pierre Fermat kuramının kanıtı, Edwin Drood'un yazılmamış bölümleri, bu bölümlerin Garamant dilindeki karşılığı, Berkeley'in Time'a ilişkin kurguladığı ancak yayımlamadığı çatışkılar, Urizen'in demir kitapları, Stephen Dedalus'un olgunlaşmamış görünüşü, kutsal Basilides İncili, deniz kızlarının söylediği şarkı, kütüphanedeki kitapların tam listesi, bu listenin doğru olmadığının kanıtı. Her şey, ancak anlaşılır her sözcük için milyonlarca kakışım, karmakarışık söz ve laf kalabalığı. Her şey, ancak insanlığın ürettiği tüm yapıtlar, sersemlemiş raflar (yaşanan anı yok eden ve karmaşanın tam üstüne bastığı raflar) onlara iyi kötü bir metin sunmadan göçüp gideceklerdir."Borges'nin toplam kütüphane kavramı yazarın 1941 tarihli çok okunan "Babil Kütüphanesi" adlı öyküsünün ana hatlarını oluşturmaktadır. Öykü, birbirine bağlı altıgen bölmelerden oluşan ve alfabenin tüm harfleri ile bazı noktalama imlerinin birlikte oluşturduğu kümeden elde edilebilecek tüm yapıtları içeren dev bir kütüphaneyi konu almaktadır.
Uygulamalar ve Eleştiriler
Evrim
Thomas Huxley, adı geçen kuramın farklı bir uyarlamasını Samuel Wilberforce'la yaptığı tartışmalarda ortaya atmakla zaman zaman yanlış biçimde ilişkilendirilmektedir.Eddington'ın rakibi James Jeans 1931 yılında yayımlanan "Gizemli Evren" adlı kitabında maymun öyküsünü büyük bir olasılıkla Thomas Henry Huxley'i kastederek bir "Huxley" ile ilişkilendirmiştir. Bu ilişkinin yanlışlığı açıktır. Günümüzde de zaman zaman dile getirilen görüş, 30 Haziran 1860 tarihinde Oxford'da Britanya Bilimsel İlerleme Derneği tarafından düzenlenen bir toplantıda Huxley'in Oxford Anglikan Piskoposu ile Charles Darwin'in Türlerin Kökeni adlı yapıtı üzerinde yaptığı tartışmada kuramı örneklendirdiği savıdır. Ne var ki, herhangi bir sağlam temele dayanmayan bu görüş 1860 yılında daktilonun henüz ortaya çıkmamış olduğu da göz önüne alındığında geçersiz kılınmaktadır. Maymunların türlü nedenlerle önemli konulardan olduğu ortamda Huxley-Wilberforce tartışması insansılara ilişkin konuşmalara da tanıklık etmiştir. Piskopos, Huxley'e büyükanne ya da büyükbabasının insansılardan gelip gelmediğini sormuş ve Huxley, piskopos gibi ikiyüzlü birinin soyundan gelmektense bir insansıdan gelmiş olmayı yeğleyeceğini söylemiştir.
Başlangıçtaki karışıklığa karşın maymun ve daktilo görüşleri günümüzde evrim üzerinde yapılan tartışmalarda aynı biçimde ifade edilmektedir. Örneğin, bir Hıristiyan savunucu olarak öne çıkan Doug Powell, bir maymunun "Hamlet"i şans eseri yazmış olsa bile bu yapıtı üretmiş olamayacağını, bunun nedeninin ise maymunun iletişim becerisine sahip olmaması olduğunu öne sürmüştür. Düşünürün doğal yasaların DNA bünyesinde saklanan bilgiyi üretemeyeceğine ilişkin savı da buna koşut bir görüş olarak değerlendirilmektedir. Daha yaygın biçimde seslendirilen görüş ise Aziz John F. MacArthur'un bir amibi tenyaya dönüştürmek için gerekli mutasyonların oluşma olasılığının bir maymunun Hamlet'in kendi kendine yaptığı konuşmaları yazma olasılığı kadar düşük olduğuna ilişkin savıdır. Buna göre, herhangi bir yaşam türü için ortaya atılan evrim iddialarının hiçbir geçerliliği yoktur.
Evrimsel biyolog Richard Dawkins yazı yazan maymun kavramını 1986'da yayımlanan Kör Saatçi adlı kitabında işlemiş ve doğal seçilimin gelişigüzel mutasyonlarla biyolojik çeşitlilik oluşturma yeteneğini göstermeye çalışmıştır. Dawkins kendi ürettiği samur programını kullanarak Hamlet metninde geçen "METHINKS IT IS LIKE A WEASEL" tümcesini oluşturmayı başarmıştır. Rastgele seçtiği bir atadan türeyen kuşakları "besleyip" atayla birebir aynı soyları seçen Dawkins rastgele mutasyonlar yaratabilmiştir. Rastgele seçimler ham bilgi üretirken art arda sıralanan tüm seçimler asıl bilgiyi açığa çıkarmaktadır.
Evrim ve sınır tanımaksızın yazı yazmasına izin verilen maymun arasında kurulan ilişkiyi geri çevirmenin bir diğer yolu ise maymunun karakterleri tek tek ve birbirinden bağımsız biçimde yazması olgusu içinde gizlidir. Biyolojik evrimden çok düşünce evrimine odaklanan Hugh Petrie daha karmaşık bir kuruluma gerek olduğunu savunmaktadır:
"Kavramlar arasındaki bağlantıyı tam olarak kurabilmek için maymuna daha karmaşık bir daktilo sunmamız gerekir. Bu daktilo Elizabeth'in tümcelerini, düşüncelerini, insan eylem biçimlerine ilişkin inançlarını ve bunların nedenlerini, Elizabeth ahlakını ve bilimini ve bunları ifade etmeye yarayan dil araçlarını içermelidir. Bu daktilonun Shakespeare'in inanç sistemini biçimlendiren deneyimlere sahip olması da beklenebilir. Tüm bunların ardından daktiloyla oynamasına izin verilen maymunun Shakespeare'in yapıtlarından birini yazması artık sürpriz olmayacaktır. Değişen şey halihazırda kazanılmış bilgi birikimidir."Klasik işlemin olanaksız olduğunu kabul eden James W. Valentine yazılı İngilizce ve metazoa genomu arasında kaydadeğer bir ilişki bulunduğunu ortaya koymuştur. Bu iki kavram arasındaki temel benzerlik ikisinin de alfabe düzeyindeki bileşim sayısını azaltan "tümleşik ve hiyerarşik yapılar" içermesidir.
Yazın Kuramı
R. G. Collingwood 1938'de sanatın şans eseri üretilemeyeceğini öne sürmüş ve eleştirilerini iğneleyici bir biçimde dile getirmiştir.
"Kimileri bu önermeyi geri çeviriyor ve bir maymuna daktilo verilirse onun Shakespeare'in tüm yapıtlarını yazabileceği görüşünü öne çıkarıyorlar. Boş zamanı olan biri bu olasılığın üzerinde tartışılmaya değer olup olmadığını anlayabilir. Önermedeki ilginç nokta, Shakespeare'in 'yapıtlarını' bir kitapta basılı karakterler olarak ayırt edebilen birinin zihinsel durumunun ortaya konmasıdır…"Nelson Goodman karşıt görüşü benimsemiş ve Borges'nin "Don Kişot'un Yazarı Pierre Menard" adlı yapıtından esinlenerek Catherine Elgin'e koşut davranmıştır.
"Menard'ın yazdığı, metnin farklı biçimdeki kaydından başka bir şey değil. Bunu herhangi birimiz, çıktı alırken ya da fotokopi çekerken yaptığı gibi, başarabilir. Öte yandan bize söylenen, sonsuz sayıda maymun … bunlardan birinin belirli bir metni birebir kopyalayabileceği. Bu kopya Cervantes'in Don Kişot adlı özgün metni, Menard'ın yapıtı ve kitabın geçmişte yazılmış ya da gelecekte yazılacak olan herhangi bir kopyası kadar geçerli olacaktır."Goodman bir başka yazıda "maymunun yapıtı rastgele yazacak oluşunun bir şeyi değiştirmeyeceğini, metnin aynı olduğunu, bu nedenle özgün metne ilişkin yorumların bu kopyaya birebir uygulanabileceğini" belirtmektedir. Gérard Genette Goodman'in bu görüşüne karşı çıkmaktadır.
Jorge J. E. Gracia elde edilen metinlerin birebir aynı oluşunun bir yazar sorunu oluşturduğunu düşünmektedir. Herhangi bir anlamlandırma amacı gütmeyen bir maymun "Hamlet" ölçeğinde bir yapıtı birebir yazabiliyorsa metinlerin yazarlara olan gereksinimi ortadan kalkacaktır. Olası çözümler, metni bulan ve onu "Hamlet" olarak adlandıranın yazar olduğu ya da Shakespeare'in yazar, maymunun yardımcı, metni bulanın ise okuyucu olduğu görüşünü benimsemektir. Ne var ki, bu çözümlerin bazı sorunları bulunmaktadır. Maymunun yapıtı Shakespeare doğmadan önce yazmış olması, Shakespeare'in hiç doğmamış olması ya da maymunun ürettiği metnin hiçbir zaman bulunmamış olması durumları olası sorunlardandır.
Rastgele Sayı Üretimi
Kuram, zaman ve kaynak tüketimi bakımından uygulanması olanaksız olan bir düşünce deneyini konu edinmektedir. Buna karşın, kuramın rastgele metin üretimindeki yeri tartışmasızdır.
The New Yorker'da yer alan bir yazıya göre Scottsdale, Arizonalı bir araştırmacı olan Dan Oliver tarafından çalıştırılan bir bilgisayar programı 4 Ağustos 2004 tarihinde sonuç vermiştir. 42.162.500.000 milyar milyar maymun yılı boyunca çalışan deney öbeği içinde yer alan bir maymun,
"VALENTINE. Cease toIdor:eFLP0FRjWK78aXzVOwm)-‘;8.t"yazısını üretmiştir. Bu dizinin ilk 19 harfi "Veronalı İki Adam" adlı kitapta yer almaktadır. Diğer maymunlar ise "Atina Dümeni"nden 18, "Troilus ve Cressida"dan 17, "II. Richard"dan 16 karakteri birebir yazabilmişlerdir.
"Maymun Shakespeare Simülatörü" adıyla 1 Temmuz 2003 tarihinde açılan web sitesi rastgele metinler üreten büyük bir maymun topluluğunu taklit eden bir Java uygulaması içermektedir. Uygulamanın amacı maymunların Shakespeare'in herhangi bir yapıtını ne kadar sürede yazabileceklerini ortaya çıkarmaktır. Örneğin, uygulamanın "IV. Henry, 2. Bölüm" adlı oyunda yer alan şu satırı üretmesi "2.737.850 milyon milyar milyar milyar maymun yılı" sürmüştür:
RUMOUR. Open your ears; 9r"5j5&?OWTY Z0d...Kısıtlı işlem gücü nedeniyle program rastgele bir metin üretip bunu Shakespeare'in yapıtlarıyla karşılaştırmak yerine olasıcı bir model uygulamaktadır (bir rastgele sayı üreteci (RSÜ) yardımıyla). Simülatör "bir eşleme bulur bulmaz" (RSÜ belirli bir değeri ürettiğinde) eşlenen metni üretmekte ve eşlemeyi bu yolla gerçekleştirmektedir.
İdeal bir maymunun belirli dizileri hangi sıklıkla yazması gerektiğini ele alan istatistiklere ilişkin sorular rastgele sayı üreteçleri için yapılan uygulamalı deneyleri de tetikleyebilmektedir. En basitten "oldukça karmaşığa" dek uzanan bu deneyler berimsel bilimler profesörleri George Marsaglia ve Arif Zaman'a göre "çakışan mli testler" olarak adlandırılmaktadır. Ne var ki, bunlsrın "maymun testleri" olarak adlandırılmasının öğrencilerin konuya olan ilgilerini artırdığı düşünülmektedir. Adı geçen biliminsanlarının farklı test sınıfları ve sonuçlarına ilişkin 1993'te yayımladıkları bir raporları bulunmaktadır.
Gerçek Maymunlar
Primat davranışçıları Cheney ve Seyfarth gerçek maymunların Romeo ve Juliet adlı yapıtı yazabilmeleri için şansa gerek duyduklarını belirtmektedir. İnsansılar ve şempanzelerden farklı olarak maymunlar bir zihin kuramına sahip olmamakta ve kendi bilgi, duygu ve inançlarıyla başkalarınınkiler arasında bir ayrım yapamamaktadırlar. Bir maymun oyun yazmayı öğrense ve kurguladığı karakterlerin davranışlarını tanımlayabilse bile bu karakterlerin zihinlerini açığa çıkaramayacağı için ortaya konan yapıt alaycı bir trajedi olacaktır.
Plymouth Üniversitesi öğretim üyeleri ve öğrencilerinden oluşan bir çalışma öbeği 2003 yılında gerçek maymunların yazınsal üretimini araştırmak üzere Sanat Kurulu'ndan 2000 sterlinlik bir ödenek almıştır. Araştırmacılar Devon, İngiltere'deki Paignton Hayvanat Bahçesi'nde bulunan altı sorguçlu kara şebeğin önüne bir klavye bırakmış ve sonuçları bir web sitesi üzerinde yayınlayabilmek için bir radyo bağlantısı kurmuşlardır. Takım üyelerinden Mike Phillips bu deneyimi "heyecan verici ve muhteşem bir şölen" olarak değerlendirmektedir.
Maymunlar, çoğunluğu S harfinden oluşan ve yalnızca beş sayfa uzunluğunda bir üretim yapmakla kalmamış, baba maymun klavyeyi bir taşla ezmeye çalışırken diğer maymunlar çiş ve kakalarını klavye üzerine yapmaktan çekinmemişlerdir. Hayvanat bahçesi fen müdürü bu deneyin "bilimsel geçerliliğinin olmadığını ve yalnızca 'sonsuz maymun' kuramının hatalı olduğunu gösterdiğini" belirtmiştir. Philips, sanat camiası tarafından desteklenen bu projenin temelde bir gösteri sanatı olduğunu ve bundan çok şey öğrendiklerini söylemiştir. Araştırmacı sözlerini şöyle sürdürmüştür:
"Maymunlar rastgele üreteç değiller, belki bunlardan daha karmaşık bir yapıya sahipler… Ekranla ilgilendiler ve klavyenin tuşuna bastıklarında bir şeyin değiştiğini gözlemleyebildiler. Belirli bir niyetleri var gibiydi."Popüler Kültürde Sonsuz Maymun Kuramı
Sonsuz maymun kuramı ve oluşturduğu imge olasılığın matematiğinin popüler ve ünlü bir ifadesi olarak kabul edilmektedir. Kavramın kamuoyunca tanınmasını sağlayan temel etken sınıf yerine popüler kültür aracılığıyla yayılmasıdır.
Kurama Douglas Adams'ın "Otostopçunun Galaksi Rehberi" adlı romanında bir şaka olarak değinilmiştir.
İlk kez 11.03.1993 tarihinde yayınlanan Amerikan çizgi dizisi "The Simpsons"ın "Last Exit to Springfield" adlı bölümünde Bay Burns şöyle konuşmaktadır:
"İşte bin daktiloda yazı yazmakta olan bin maymun. Yakında şu ana dek yazılmış en iyi romanı kaleme almış olacaklar. Bakalım. Seni aptal maymun!"Kurama ilişkin bilgi birikiminin dayanıklı, yaygın ve popüler doğası 2001 yılında yayımlanan "Maymunlar, Daktilolar ve Ağlar: Kaza Eseri Elde Edilen Mükemmellik Kuramı Işığında İnternet" (Hoffmann & Hofmann) adlı bir makalenin girişinde yer almıştır. Washington Post adlı Amerikan gazetesinin 2002 tarihli bir sayısında şöyle denilmektedir:
"Birçok kişi sonsuz sayıda maymunun sonsuz sayıda daktilo kullanarak sonsuz bir zaman dilimi içinde Shakespeare'in yapıtlarını elde edeceğine ilişkin ünlü kuramla eğlendi."İngiltere Sanat Kurulu tarafından desteklenen ve 2003 yılında gerçekleştirilen deney ise basından büyük ilgi görmüştür. Kuram 2007 yılında Wired dergisi tarafından sekiz klasik düşünce deneyinden biri olarak gösterilmiştir.
Çizer Ruben Bolling düşünce deneyini "Tom the Dancing Bug" adlı çizgi filmde bir maymuna söylettiği şu sözlerle taşlamıştır:
"Hamlet'in öcünü beşinci perdeye dek nasıl geciktirebilirim?"David Ives'ın 1987'de yazmış olduğu "Words, Words, Words" adlı oyun sonsuz maymun kuramında yer alan üç maymun arasında geçen karşılıklı konuşmaları ele almaktadır. Oyun, maymunlardan birinin "Hamlet"in ilk satırlarını yazarken diğer ikisinin rastgele metinler üretmesiyle sonlanmaktadır.
Tanrı varsa eğer, ruhumu kutsasın... Ruhum varsa eğer!
