Rassal değişken
Vikipedi, özgür ansiklopedi
Rassal değişken kavramının geliştirilmesi ile, sezgi yoluyla anlaşılan şans kavramı, soyutlaştırarak teorik matematik analiz alanına sokulmuş ve bu geliştirilen matematik kavram ile olasılık kuramı ve matematiksel istatistikin temeli kurulmuştur.
Son birkaç yüzyılda olasılıkla ilgili matematiksel fikirler geliştirilirken rassal değişkenlerlerle ilişkili teori ve kullanım matematik kuramı biçimlerine konulmuştur. Rassal değişkenleri modern matematik görüşle tam olarak anlamak için, daha yakın zamanlarda matematikçiler tarafından geliştirilmiş olan ölçüm kuramı hakkında geniş bilginin kazanılması gerekmektedir. Rassal değişken kavramı, bu kuram içinde tüm özellikleri ile arka planda kalmakla beraber, kuramın içeriğinde önemli bir yeri bulunmaktadır. Bununla beraber, rassal değişkenler kavramının matematiksel teoride değişik ileri seviyelerde fazla teori gerektirmeyen çok daha az ileri matematiksel bilgisi ile de anlaşılması mümkündür. Böylece rassal değişkenler hakkında temel bilgileri anlamak için sadece set kuramı ve değişkenler hesabının bilinmesi yeterli olmaktadır.
Geniş bir tanımlama ile, bir rassal değişken, değerleri rassal olan ve bu değerler için bir olasılık dağılımı saptamak imkânı olan bir sayıdır. Daha matematiksel biçimde, bir rassal değişken bir örneklem uzayından dağişkenin mümkün değerlerinden oluşan ölçülebilir uzaya değişimi gösterir. Rassal değiskenlerin bu formel tanımlanması reel değerli sonuçlar veren deneyleri çok sıkı bir surette matematiksel ölçüm kuramı çerçevesi içine sokmakta ve reel değerli rassal değişkenler için dağılım fonksiyonu kurulmasına imkân sağlamaktadır.
Sezgisel tanımlama
Genellikle bir rassal değişken sayı şeklinde değerler alır. Ama bu her zaman doğru değildir; çünkü vektör, karmaşık sayılar, sıralamalar veya fonksiyonlardan oluşan rassal değişkenler bulunmaktadır. Eğer değişkenler reel-değerli iseler o zaman bir rassal değişken her ele alınıp incelendiği zaman değer değiştirebilen bir bilinmez sayı olarak düşünülebilir. Böylece bir rassal değişken bir rasgele sürecinin örnek uzayını bir sayı setine eşlemesini yapan bir fonksiyon olarak görülebilir. Bunu daha göze çarpar bir şekilde şu örneğinlerle gösterebiliriz:
Örnekler
Hileli olmayan bir metal parayı havaya atma ve hangi yuzu gelecegini ele alma deneyini once ele alalım. Tek bir deney icin mumkun sonuc olaylar ya "yazı" ya da "tura" olur. Birkac defa para atılması ve bunlardan kac tane yazi gelecegi su rassal degisken ile ifade edilebilir:

ve eger metal para icin bu iki sonuc esit olabilirlikli ise o zaman bu rassal degisken icin bir olasılık kütle fonksiyunu bulunur ve soyle ifade edilir:
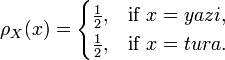
Bazan daha kolaylık saglamak icin bu haldeki degerler olarak ("yazı" veya "tura" kategorileri yerine) sayılar seklinde olan bir rassal degisken tanımlanabilir. Bunu Y reel rassal degiskenini kullanarak ve bunu su sekilde tanımlayarak yapabiliriz:

ve eğer metal para için bu iki sonuç için her iki taraf eşit olabilirlikli ise o zaman olasılık kütle fonksiyunu şöyle ifade edilir:

Bir rassal ayrık rassal değişken kavramı kullanılması için diğer bir örneğin, hileli olmayan bir zar atılması ve düşen zarda üste gelen nokta sayısını görme şeklindeki deneyidir. Bu halde en basit açıklama, olası sonuçlar olan { 1, 2, 3, 4, 5, 6 } sayıları setinin "örnek uzayı" ve zar atınca gelen sayı X'in de rassal değişken şeklinde yapılabilir. Bu halde

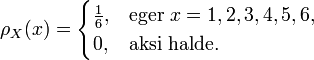
Bir surekli rasal degisken icin bir ornek sonunda belli bir yone yonelip kalan bir doner ibreli aletin ibresi ele alinabilir. Bu orneginde rassal degisken tarafindan sonuc degrelr yonlerdir. Bu yonler ayrik olarak Kuzey bati, Dogu guney dogu vb. sekilde iifade edilebilirler. Fakat genellikle ornek uzayini bir rassal degiskene eslendirilmesi yapilirken reel sayilar kullanmak dah kullanisli olacaktir. Bunu basarmak icin doner ibreini son durma yonunu Kuzey'den olan saat yonundeki acisinin derece birimi ile ifade edebiliriz. Boylece rassal degisken [O, 360]] araliginda herhangi bir sayi sekilde ifade edilir ve her bir mumkun sayinin acikligi rasgelirligi "esit olasilikli"dir. Bu halde rassal degisken X= ibre durus acisi olur. Herhangi bir belirli sayinin olasigi 0 olur ama bir sayisal aralik icin bir pozitif olasilik sayisi verilebilir. Ornegin, [0,180]] arasinda bir sayinin geleme olasigi ½ olur. Bu halde olasilik kutle yogunluk fonkisyonu demeyiz ama X' icin olasilik yogunlugu 1/360 olur. (0, 360) alt-seti icin olasilik bu setin olcusunu 1/360 ile carpma ile elde edilir. Genel olarak, bir belirlenmeis surekli rassal degisken seti icin olasilik yogunlugun verilmis set uzerinde entegrasyonunu bulmak suretiyle elde edilir.
Karisik ayrik ve surekli rassal degisken icin ornegin bir matal parayi atmak ile egr para "yazi" gelmisse bir doner ibreli aletin ibresini dondurmek seklinde verilebilir. Bu deneyin sonucunu matematiksel ifadesi soyle olur: Eger para atis "tura" gelirse X= -1; aksi halde X' doner ibreli aletin ibresinin durdugunda gosterdigi yonun Kuzeye gore saat yonundeki aci degeridir. Bu ikili deney icin rassal degisken degerinin -1 olamasi olasigi ½ olur; diger araliklar icin rasal degisken degerleri bir onceki deneyiin sonuclarainin yarisina esittir.
Sponsorlu Bağlantılar
Rassal değişken kavramının geliştirilmesi ile, sezgi yoluyla anlaşılan şans kavramı, soyutlaştırarak teorik matematik analiz alanına sokulmuş ve bu geliştirilen matematik kavram ile olasılık kuramı ve matematiksel istatistikin temeli kurulmuştur.
Son birkaç yüzyılda olasılıkla ilgili matematiksel fikirler geliştirilirken rassal değişkenlerlerle ilişkili teori ve kullanım matematik kuramı biçimlerine konulmuştur. Rassal değişkenleri modern matematik görüşle tam olarak anlamak için, daha yakın zamanlarda matematikçiler tarafından geliştirilmiş olan ölçüm kuramı hakkında geniş bilginin kazanılması gerekmektedir. Rassal değişken kavramı, bu kuram içinde tüm özellikleri ile arka planda kalmakla beraber, kuramın içeriğinde önemli bir yeri bulunmaktadır. Bununla beraber, rassal değişkenler kavramının matematiksel teoride değişik ileri seviyelerde fazla teori gerektirmeyen çok daha az ileri matematiksel bilgisi ile de anlaşılması mümkündür. Böylece rassal değişkenler hakkında temel bilgileri anlamak için sadece set kuramı ve değişkenler hesabının bilinmesi yeterli olmaktadır.
Geniş bir tanımlama ile, bir rassal değişken, değerleri rassal olan ve bu değerler için bir olasılık dağılımı saptamak imkânı olan bir sayıdır. Daha matematiksel biçimde, bir rassal değişken bir örneklem uzayından dağişkenin mümkün değerlerinden oluşan ölçülebilir uzaya değişimi gösterir. Rassal değiskenlerin bu formel tanımlanması reel değerli sonuçlar veren deneyleri çok sıkı bir surette matematiksel ölçüm kuramı çerçevesi içine sokmakta ve reel değerli rassal değişkenler için dağılım fonksiyonu kurulmasına imkân sağlamaktadır.
Sezgisel tanımlama
Genellikle bir rassal değişken sayı şeklinde değerler alır. Ama bu her zaman doğru değildir; çünkü vektör, karmaşık sayılar, sıralamalar veya fonksiyonlardan oluşan rassal değişkenler bulunmaktadır. Eğer değişkenler reel-değerli iseler o zaman bir rassal değişken her ele alınıp incelendiği zaman değer değiştirebilen bir bilinmez sayı olarak düşünülebilir. Böylece bir rassal değişken bir rasgele sürecinin örnek uzayını bir sayı setine eşlemesini yapan bir fonksiyon olarak görülebilir. Bunu daha göze çarpar bir şekilde şu örneğinlerle gösterebiliriz:
Örnekler
Hileli olmayan bir metal parayı havaya atma ve hangi yuzu gelecegini ele alma deneyini once ele alalım. Tek bir deney icin mumkun sonuc olaylar ya "yazı" ya da "tura" olur. Birkac defa para atılması ve bunlardan kac tane yazi gelecegi su rassal degisken ile ifade edilebilir:

ve eger metal para icin bu iki sonuc esit olabilirlikli ise o zaman bu rassal degisken icin bir olasılık kütle fonksiyunu bulunur ve soyle ifade edilir:
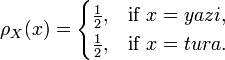
Bazan daha kolaylık saglamak icin bu haldeki degerler olarak ("yazı" veya "tura" kategorileri yerine) sayılar seklinde olan bir rassal degisken tanımlanabilir. Bunu Y reel rassal degiskenini kullanarak ve bunu su sekilde tanımlayarak yapabiliriz:

ve eğer metal para için bu iki sonuç için her iki taraf eşit olabilirlikli ise o zaman olasılık kütle fonksiyunu şöyle ifade edilir:

Bir rassal ayrık rassal değişken kavramı kullanılması için diğer bir örneğin, hileli olmayan bir zar atılması ve düşen zarda üste gelen nokta sayısını görme şeklindeki deneyidir. Bu halde en basit açıklama, olası sonuçlar olan { 1, 2, 3, 4, 5, 6 } sayıları setinin "örnek uzayı" ve zar atınca gelen sayı X'in de rassal değişken şeklinde yapılabilir. Bu halde

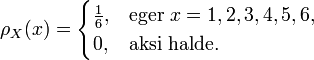
Bir surekli rasal degisken icin bir ornek sonunda belli bir yone yonelip kalan bir doner ibreli aletin ibresi ele alinabilir. Bu orneginde rassal degisken tarafindan sonuc degrelr yonlerdir. Bu yonler ayrik olarak Kuzey bati, Dogu guney dogu vb. sekilde iifade edilebilirler. Fakat genellikle ornek uzayini bir rassal degiskene eslendirilmesi yapilirken reel sayilar kullanmak dah kullanisli olacaktir. Bunu basarmak icin doner ibreini son durma yonunu Kuzey'den olan saat yonundeki acisinin derece birimi ile ifade edebiliriz. Boylece rassal degisken [O, 360]] araliginda herhangi bir sayi sekilde ifade edilir ve her bir mumkun sayinin acikligi rasgelirligi "esit olasilikli"dir. Bu halde rassal degisken X= ibre durus acisi olur. Herhangi bir belirli sayinin olasigi 0 olur ama bir sayisal aralik icin bir pozitif olasilik sayisi verilebilir. Ornegin, [0,180]] arasinda bir sayinin geleme olasigi ½ olur. Bu halde olasilik kutle yogunluk fonkisyonu demeyiz ama X' icin olasilik yogunlugu 1/360 olur. (0, 360) alt-seti icin olasilik bu setin olcusunu 1/360 ile carpma ile elde edilir. Genel olarak, bir belirlenmeis surekli rassal degisken seti icin olasilik yogunlugun verilmis set uzerinde entegrasyonunu bulmak suretiyle elde edilir.
Karisik ayrik ve surekli rassal degisken icin ornegin bir matal parayi atmak ile egr para "yazi" gelmisse bir doner ibreli aletin ibresini dondurmek seklinde verilebilir. Bu deneyin sonucunu matematiksel ifadesi soyle olur: Eger para atis "tura" gelirse X= -1; aksi halde X' doner ibreli aletin ibresinin durdugunda gosterdigi yonun Kuzeye gore saat yonundeki aci degeridir. Bu ikili deney icin rassal degisken degerinin -1 olamasi olasigi ½ olur; diger araliklar icin rasal degisken degerleri bir onceki deneyiin sonuclarainin yarisina esittir.
Bir bildiğim varsa hiç bir şey bilmediğimdir. (:

 Rassal Değişken
Rassal Değişken
