Tesselasyon (Düzlemsel Şekiller Kümesi)
Vikipedi, özgür ansiklopedi
Matematikte bir döşeme (veya karolama, süsleme), aralarında boşluk bırakmadan veya örtüşmeden bir düzlemi kaplayan düzlemsel şekiller kümesidir. Bu kavram daha yüksek boyutlar için de genellenebilir, bu genişletilmiş anlamı için döşeme yerine tesselasyon terimi kullanılır. Tesselasyon M. C. Escher'in eserlerinde sıkça görülebilir. Tesselasyona sanat tarihi boyunca, antik mimariden modern sanata kadar rastlanabilir.

Latince "tessella", mozaik yapmakta kullanılan küp şekilli bir kil, taş veya cam parçasıdır. "Tessella" sözcüğü (kare anlamına gelen "tessera"dan gelir, onun kaynağı da "dört" anlamına gelen Yunanca sözcüktür) küçük kare anlamına gelir. Gündelik dilde parke, karo veya çini döşeme, bu malzemelerin tesselasyon şeklinde yere veya duvara döşenmesidir. Döşeme sözcüğü hem bu tür düzlem kaplayıcı cisim veya şekillere, hem de bu cisimlerle veya şekillerle kaplanmış yüzey için kullanılır. Anlam kargaşasına yol açmamak için, aşağıdaki metinde, düzlemi kaplayıcı şekiller için karo terimi kullanılacaktır, ama "karo"nun gündelik dildeki anlamının aksine, tessalasyon yapmakta kullanılan şekillerin dörtgen olma şartı yoktur.

Duvar kağıdı grupları
Öteleme simetrisi olan döşemeler "duvarkağıdı grubu" olarak kategorilendirilebilir, bunlardan 17 tane vardır. El Hamra Sarayı'nda bu örüntü tiplerinin her birinden bulunur. Düzgün (eşkenar çokgenlerden meydana gelen) döşemelerden ikisi p6m, biri p4m kategorisine aittir.
Tesselasyon ve renkler

Renkli bir döşemeden bahsederken, yanlış anlamaya yol açmamak için, renklerin döşemenin parçası mı olduğu yoksa sadece tekrar eden birim şekle mi ait olduğunun belirtilmesi gerekir.
Dört renk teoremi, normal bir Öklid düzlemindeki her bir döşemesi için, eğer dört renk kullanılırsa, her bir karonun komşularından farklı bir renkle boyanabileceğini önerir; bu boyamada aynı renge sahip iki karo pozitif uzunlukla bir kenar ile birbirine dokunamaz. Ancak, dört renk kuramının garantilediği renklendirme genelde tesselasyonun meydana getirdiği simetriyi muhafaza etmeyebilir. Tesselasyon simetrisine uyan bir renklendirme daha fazla sayıda renk gerektirebilir, yukarıdaki resimdeki örnekte görülebileceği gibi.
Dörtgenlerle tesselasyon
Herhangi bir dörtgen karonun kopyaları kullanılarak elde edilecek döşemenin belli simetri özellikleri vardır:
Düzgün ve yarı-düzgün tesselasyonlar

Düzenli tesselasyon, benzer düzgün çokgenlerden oluşmuş yüksek simetrili bir tesselasyondur. Sadece üç tane düzgün tesselasyon vardır. Bunlar eşkenar üçgenlerden, karelerden veya altıgenlerden meydana gelen döşemelerdir.
Yarı düzgün tesselasyonlar çeşitli düzgün çokgenlerden oluşur; bunlardan sekiz sınıf vardır. Bu çokgenlerin her bir köşedeki yerleşimi aynıdır. Kenar-kenara tesselasyonlar daha düzensizdir: tek şart, bitişik şekillerin tek bir kenarı paylaşmasıdır, yani bir şekil bir kenarının sadece bir kısmını başka bir şekille paylaşamaz. Başka tür tesselasyonlar da mevcuttur, kullanılan şekil ve bunların örüntüsüne bağlı olarak. Düzgün olan ve olmayan, periyodik ve aperiyodik (periyodik olmayan), simetrik ve asimetrik, ayrıca fraktal tesselasyonlar vardır, bunların yanı sıra başka sınıflandırmalar da sayılabilir.
İki farklı çokgen kullanan Penrose döşemesi aperiyodik örüntüler yaratan tesselasyonların en meşhur örneğidir. Bu döşemeler, özyineleme kullanarak kendi kendini üreten çokgen kümelerinden inşa edilen aperiyodik döşemeler sınıfına aittir.
Monohedral kaplama, tüm şekillerin birbirine benzer olduğu bir tesselasyondur. Spiral monohedral döşemeler arasında Hans Voderberg tarafından 1936'da keşfedilmiş olan Voderberg döşemesi ve Michael Hirschhorn tarafından 1970'lerde keşfedilen Hirschhorn döşemesi bulunmaktadır. Voderberg döşemesinin birim şekli konveks olmayan bir dokuzgen, Hirschhorn döşemesinin birim şekli ise düzgün olmayan bir beşgendir.
Öz-çifteş tesselasyonlar
Eğer bir şeklin kenarları ve köşelerinin yer değiştirmesi halinde gene aynı şekil ortaya çıkarsa (kare gibi) bu şeklin öz-çifteş (self dual) olduğu söylenebilir. Düzgün döşemeler ve petekler öz-çifteş olabilir. Schlafli sembolü ile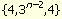 olarak betimlenen tüm n-boyutlu hiperkübik petekler öz çifteştir.
olarak betimlenen tüm n-boyutlu hiperkübik petekler öz çifteştir.
Tesselasyonlar ve bilgisayar modeleri

Bilgisayar grafiği sahasında, çokgenlerden oluşan veri kümelerinin idaresi ve onların grafik sunumu (rendering) için kullanışlı yapılara bölünmesi için sık sık tesselasyon teknikleri kullanılır. Normalde, en azından gerçek zamanlı renderingde, görüntüyü oluşturan verilerin üçgenler halinde döşemsi yapılır, bu işleme bazen üçgenleme denir. Tesselasyon, bilgisayar grafikleme arayüzlerinden DirectX 11 ve OpenGL'nin temel özelliğidir.
Bilgisayar eşlikli tasarımda oluşturulan tasarım, bir sınır temsil topoloji modeli ile temsil edilir. Bunda, yüzey ve kenarlar ile sınırlandırılmış analitik üç boyutlu yüzey ve eğriler, 3 boyutlu bir cismin kesintisiz sınırını oluşturur. Herhangi bir 3 boyutlu cisim doğrudan analiz edilemeyecek kadar karmaşık olabilir. Bu cisimler, kolay analiz edilebilen küçük 3-boyutlu hacim elemanlarından oluşan bir ağ ile kaplanır, genelde bu ağ ya düzensiz tetrahedronlar veya düzensiz heksahedronlardan oluşur. Bu ağ, sonlu eleman analizi için kullanılır.
Bir yüzeyin ağı genelde teker teker yüzey ve kenarlardan oluşturulur, öyleki ki özgün cismin yüzeyindeki limit noktalar ağın parçası olur. Özgün yüzeyin bu ağ tarafından benzetilmesi, ağı oluşturan fonksiyonun üç parametresi tarafından belirlenir.
Bazı jeodesik kubbeler, mümkün olduğunca eşkenarlı olan üçgenlerle bir kürenin yüzyeyini kaplayarak tasarlanır.
Doğada tesselasyonlar

Bazaltik lav akıntıları katılaştıktan sonra çoğu zaman büzülme kuvvetlerinin etkisiyle sütunsal çatlak yaparlar. Meydana gelen yaygın çatlak ağı genelde altıgensel lav sütunlar oluşturur. Bunun bir örneği, Kuzey İrlanda'daki Giant's Causeway'deki sütün dizilimidir.
Tazmanya'daki mozaik kaldırım taşları, kayaçların dörtgen bloklar şeklinde çatlamış olduğu ender bir tortul kayaç oluşumudur.
Vikipedi, özgür ansiklopedi
Sponsorlu Bağlantılar
Matematikte bir döşeme (veya karolama, süsleme), aralarında boşluk bırakmadan veya örtüşmeden bir düzlemi kaplayan düzlemsel şekiller kümesidir. Bu kavram daha yüksek boyutlar için de genellenebilir, bu genişletilmiş anlamı için döşeme yerine tesselasyon terimi kullanılır. Tesselasyon M. C. Escher'in eserlerinde sıkça görülebilir. Tesselasyona sanat tarihi boyunca, antik mimariden modern sanata kadar rastlanabilir.
Kaldırım parkelerinin bir tesselasyonu

Latince "tessella", mozaik yapmakta kullanılan küp şekilli bir kil, taş veya cam parçasıdır. "Tessella" sözcüğü (kare anlamına gelen "tessera"dan gelir, onun kaynağı da "dört" anlamına gelen Yunanca sözcüktür) küçük kare anlamına gelir. Gündelik dilde parke, karo veya çini döşeme, bu malzemelerin tesselasyon şeklinde yere veya duvara döşenmesidir. Döşeme sözcüğü hem bu tür düzlem kaplayıcı cisim veya şekillere, hem de bu cisimlerle veya şekillerle kaplanmış yüzey için kullanılır. Anlam kargaşasına yol açmamak için, aşağıdaki metinde, düzlemi kaplayıcı şekiller için karo terimi kullanılacaktır, ama "karo"nun gündelik dildeki anlamının aksine, tessalasyon yapmakta kullanılan şekillerin dörtgen olma şartı yoktur.
Bir arı peteği tesselasyonlu bir doğal yapı örneğidir.

Duvar kağıdı grupları
Öteleme simetrisi olan döşemeler "duvarkağıdı grubu" olarak kategorilendirilebilir, bunlardan 17 tane vardır. El Hamra Sarayı'nda bu örüntü tiplerinin her birinden bulunur. Düzgün (eşkenar çokgenlerden meydana gelen) döşemelerden ikisi p6m, biri p4m kategorisine aittir.
Tesselasyon ve renkler
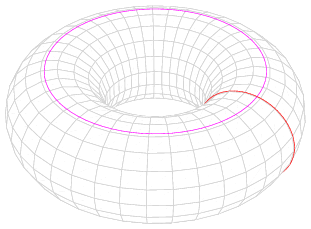
Bu paralelkenar örüntüsü bir düzlemi kaplamadan önce boyanırsa, her bir paralelkenarın komşularından farklı bir renge sahip olabilmesi için yedi farklı renk kullanılması gerekir. (Bu döşeme şekli bir simit yüzeyinin döşenmesine benzetilebilir). Eğer döşeme boyamadan önce yapılırsa sadece dört renk yeterlidir.

Renkli bir döşemeden bahsederken, yanlış anlamaya yol açmamak için, renklerin döşemenin parçası mı olduğu yoksa sadece tekrar eden birim şekle mi ait olduğunun belirtilmesi gerekir.
Dört renk teoremi, normal bir Öklid düzlemindeki her bir döşemesi için, eğer dört renk kullanılırsa, her bir karonun komşularından farklı bir renkle boyanabileceğini önerir; bu boyamada aynı renge sahip iki karo pozitif uzunlukla bir kenar ile birbirine dokunamaz. Ancak, dört renk kuramının garantilediği renklendirme genelde tesselasyonun meydana getirdiği simetriyi muhafaza etmeyebilir. Tesselasyon simetrisine uyan bir renklendirme daha fazla sayıda renk gerektirebilir, yukarıdaki resimdeki örnekte görülebileceği gibi.
Dörtgenlerle tesselasyon
Herhangi bir dörtgen karonun kopyaları kullanılarak elde edilecek döşemenin belli simetri özellikleri vardır:
- Her bir dörtgen kenarının orta noktasında iki katlı dönel simetrisi vardır.
- Dörtgenlerin gösterdiği öteleme simetrisinin taban vektörleri ya
- Dörtgenin köşegenleri veya
- Köşegenlerden biri ve iki köşegenin toplamı veya farkıdır.
Düzgün ve yarı-düzgün tesselasyonlar
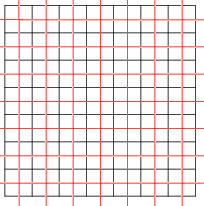
Döşemede altıgenlerden oluşan bir tesselasyon

Düzenli tesselasyon, benzer düzgün çokgenlerden oluşmuş yüksek simetrili bir tesselasyondur. Sadece üç tane düzgün tesselasyon vardır. Bunlar eşkenar üçgenlerden, karelerden veya altıgenlerden meydana gelen döşemelerdir.
Yarı düzgün tesselasyonlar çeşitli düzgün çokgenlerden oluşur; bunlardan sekiz sınıf vardır. Bu çokgenlerin her bir köşedeki yerleşimi aynıdır. Kenar-kenara tesselasyonlar daha düzensizdir: tek şart, bitişik şekillerin tek bir kenarı paylaşmasıdır, yani bir şekil bir kenarının sadece bir kısmını başka bir şekille paylaşamaz. Başka tür tesselasyonlar da mevcuttur, kullanılan şekil ve bunların örüntüsüne bağlı olarak. Düzgün olan ve olmayan, periyodik ve aperiyodik (periyodik olmayan), simetrik ve asimetrik, ayrıca fraktal tesselasyonlar vardır, bunların yanı sıra başka sınıflandırmalar da sayılabilir.
İki farklı çokgen kullanan Penrose döşemesi aperiyodik örüntüler yaratan tesselasyonların en meşhur örneğidir. Bu döşemeler, özyineleme kullanarak kendi kendini üreten çokgen kümelerinden inşa edilen aperiyodik döşemeler sınıfına aittir.
Monohedral kaplama, tüm şekillerin birbirine benzer olduğu bir tesselasyondur. Spiral monohedral döşemeler arasında Hans Voderberg tarafından 1936'da keşfedilmiş olan Voderberg döşemesi ve Michael Hirschhorn tarafından 1970'lerde keşfedilen Hirschhorn döşemesi bulunmaktadır. Voderberg döşemesinin birim şekli konveks olmayan bir dokuzgen, Hirschhorn döşemesinin birim şekli ise düzgün olmayan bir beşgendir.
Öz-çifteş tesselasyonlar
Eğer bir şeklin kenarları ve köşelerinin yer değiştirmesi halinde gene aynı şekil ortaya çıkarsa (kare gibi) bu şeklin öz-çifteş (self dual) olduğu söylenebilir. Düzgün döşemeler ve petekler öz-çifteş olabilir. Schlafli sembolü ile
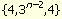 olarak betimlenen tüm n-boyutlu hiperkübik petekler öz çifteştir.
olarak betimlenen tüm n-boyutlu hiperkübik petekler öz çifteştir.
Tesselasyonlar ve bilgisayar modeleri
Sonlu elemanlar problemini çözmek için bir diskin tesselasyonu

Bilgisayar grafiği sahasında, çokgenlerden oluşan veri kümelerinin idaresi ve onların grafik sunumu (rendering) için kullanışlı yapılara bölünmesi için sık sık tesselasyon teknikleri kullanılır. Normalde, en azından gerçek zamanlı renderingde, görüntüyü oluşturan verilerin üçgenler halinde döşemsi yapılır, bu işleme bazen üçgenleme denir. Tesselasyon, bilgisayar grafikleme arayüzlerinden DirectX 11 ve OpenGL'nin temel özelliğidir.
Bilgisayar eşlikli tasarımda oluşturulan tasarım, bir sınır temsil topoloji modeli ile temsil edilir. Bunda, yüzey ve kenarlar ile sınırlandırılmış analitik üç boyutlu yüzey ve eğriler, 3 boyutlu bir cismin kesintisiz sınırını oluşturur. Herhangi bir 3 boyutlu cisim doğrudan analiz edilemeyecek kadar karmaşık olabilir. Bu cisimler, kolay analiz edilebilen küçük 3-boyutlu hacim elemanlarından oluşan bir ağ ile kaplanır, genelde bu ağ ya düzensiz tetrahedronlar veya düzensiz heksahedronlardan oluşur. Bu ağ, sonlu eleman analizi için kullanılır.
Bir yüzeyin ağı genelde teker teker yüzey ve kenarlardan oluşturulur, öyleki ki özgün cismin yüzeyindeki limit noktalar ağın parçası olur. Özgün yüzeyin bu ağ tarafından benzetilmesi, ağı oluşturan fonksiyonun üç parametresi tarafından belirlenir.
- Gerçek yüzey ile düzlemsel yaklaşıklık arasındaki en büyük uzaklık ("sarkma" tabir edilir). Bu parametre ağın özgün yüzeye yeterince benzemesini sağlar.
- Benzetme çokgeninin en büyük boyu. Bu parametre daha ayrıntılı analiz için yeterince detay kalmasını sağlar.
- İki benzetme çokgeni arasındaki en büyük düzlemsel açı. Bu parametre çok küçük tümsek veya oyukların ağ içinde kaybolmamasını saplar.
Bazı jeodesik kubbeler, mümkün olduğunca eşkenarlı olan üçgenlerle bir kürenin yüzyeyini kaplayarak tasarlanır.
Doğada tesselasyonlar
Gün batımında mozaik kaldırım taşı biçiminde kayalar. Eaglehawk Neck, Tazmanya.

Bazaltik lav akıntıları katılaştıktan sonra çoğu zaman büzülme kuvvetlerinin etkisiyle sütunsal çatlak yaparlar. Meydana gelen yaygın çatlak ağı genelde altıgensel lav sütunlar oluşturur. Bunun bir örneği, Kuzey İrlanda'daki Giant's Causeway'deki sütün dizilimidir.
Tazmanya'daki mozaik kaldırım taşları, kayaçların dörtgen bloklar şeklinde çatlamış olduğu ender bir tortul kayaç oluşumudur.
Tanrı varsa eğer, ruhumu kutsasın... Ruhum varsa eğer!

 Tesselasyon (Düzlemsel Şekiller Kümesi)
Tesselasyon (Düzlemsel Şekiller Kümesi)

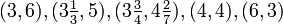
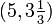 değerleri kullanılır.
değerleri kullanılır.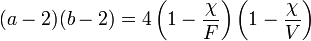
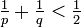 ise, p-kenarlı şekillerden q tanesinin birbirine değdiği bir tesselasyona izin verir. Circle Limit III, üçlüler halinde bir araya gelen sekizgenlerin bir döşemesi olarak anlaşılabilir, resimde kenarların herbiri yerine pürüzlü çizgiler yer almaktadır ve her sekizgen dört balığa bölünmüştür.
ise, p-kenarlı şekillerden q tanesinin birbirine değdiği bir tesselasyona izin verir. Circle Limit III, üçlüler halinde bir araya gelen sekizgenlerin bir döşemesi olarak anlaşılabilir, resimde kenarların herbiri yerine pürüzlü çizgiler yer almaktadır ve her sekizgen dört balığa bölünmüştür.