Vektör Uzayı
MsXLabs & Morpa Genel Kültür Ansiklopedisi & Vikipedi
Vektör uzayı, matematikte ölçeklenebilir ve eklenebilir bir nesneler (vektörler) topluluğu.
Daha resmi bir tanımla, bir vektör uzayı, üzerinde vektör ekleme (toplama) ve ölçeksel çarpma adı verilen iki işlemin yapılabildiği ve bunların bazı aksiyomları sağladığı kümedir. Bir vektör kümesiyle bir skaler alanının bir araya gelmesiyle oluşan matematiksel uzay. Bunun için, kümenin herhangi iki elemanının toplamı yine kümede eleman olan bir vektör vermeli ve kümenin herhangi bir elemanının herhangi bir skalerle çarpımı da yine kümede eleman olmalıdır. Vektör uzayı lineer cebirde çokça kullanılır.
K bir cisim ve (V, + ,0) bir abelyen grup olsun. Ayrıca 'den V'ye giden bir fonksiyonun varlığını varsayalım. Eğer
'den V'ye giden bir fonksiyonun varlığını varsayalım. Eğer 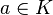 ve
ve  ise, bu fonksiyonun (a,v)çiftinde aldığı değeri av olarak yazalım. Bütün bunlar şu özellikleri sağlasın: Her
ise, bu fonksiyonun (a,v)çiftinde aldığı değeri av olarak yazalım. Bütün bunlar şu özellikleri sağlasın: Her 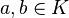 ve
ve  için
için
V1. a(v + w) = av + aw,
V2. (a + b)v = av + bv,
V3. (ab)v = a(bv),
V4. 1v = v.
O zaman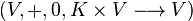 yapısına K üzerine bir vektör uzayı adı verilir. V kümesinin elemanlarına vektör denir.
yapısına K üzerine bir vektör uzayı adı verilir. V kümesinin elemanlarına vektör denir.
Eğer K bir cisimse ve n bir doğal sayıysa, Kn kümesi,
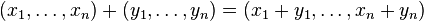
işlemiyle ve
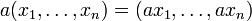 işlemiyle bir vektör uzayıdır.
işlemiyle bir vektör uzayıdır.
Burada Kn yerine K'nın herhangi bir kartezyen çarpımını alabiliriz ve vektör uzayı yapısını benzer biçimde (koordinat koordinat) tanımlayabiliriz.
MsXLabs & Morpa Genel Kültür Ansiklopedisi & Vikipedi
Sponsorlu Bağlantılar
Vektör uzayı, matematikte ölçeklenebilir ve eklenebilir bir nesneler (vektörler) topluluğu.
Daha resmi bir tanımla, bir vektör uzayı, üzerinde vektör ekleme (toplama) ve ölçeksel çarpma adı verilen iki işlemin yapılabildiği ve bunların bazı aksiyomları sağladığı kümedir. Bir vektör kümesiyle bir skaler alanının bir araya gelmesiyle oluşan matematiksel uzay. Bunun için, kümenin herhangi iki elemanının toplamı yine kümede eleman olan bir vektör vermeli ve kümenin herhangi bir elemanının herhangi bir skalerle çarpımı da yine kümede eleman olmalıdır. Vektör uzayı lineer cebirde çokça kullanılır.
K bir cisim ve (V, + ,0) bir abelyen grup olsun. Ayrıca
 'den V'ye giden bir fonksiyonun varlığını varsayalım. Eğer
'den V'ye giden bir fonksiyonun varlığını varsayalım. Eğer 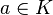 ve
ve  ise, bu fonksiyonun (a,v)çiftinde aldığı değeri av olarak yazalım. Bütün bunlar şu özellikleri sağlasın: Her
ise, bu fonksiyonun (a,v)çiftinde aldığı değeri av olarak yazalım. Bütün bunlar şu özellikleri sağlasın: Her 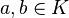 ve
ve  için
için V1. a(v + w) = av + aw,
V2. (a + b)v = av + bv,
V3. (ab)v = a(bv),
V4. 1v = v.
O zaman
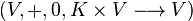 yapısına K üzerine bir vektör uzayı adı verilir. V kümesinin elemanlarına vektör denir.
yapısına K üzerine bir vektör uzayı adı verilir. V kümesinin elemanlarına vektör denir.Eğer K bir cisimse ve n bir doğal sayıysa, Kn kümesi,
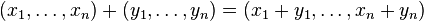
işlemiyle ve
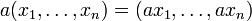 işlemiyle bir vektör uzayıdır.
işlemiyle bir vektör uzayıdır.Burada Kn yerine K'nın herhangi bir kartezyen çarpımını alabiliriz ve vektör uzayı yapısını benzer biçimde (koordinat koordinat) tanımlayabiliriz.
"İnşallah"derse Yakaran..."İnşa" eder YARADAN.

 Vektör Uzayı
Vektör Uzayı
