Üstel Fonksiyon
VIP VIP Üye
Üstel Fonksiyon
MsXLabs.org & Morpa Genel Kültür Ansiklopedisi & Vikipedi
Üstel fonksiyon, matematiğin en önemli fonksiyonlarından biridir. ex veya exp(x) sembolleriyle gösterilir. Burada e, yaklaşık değeri 2,718 olan Euler sayısını temsil eder, x ise gerçel ya da karmaşık bir değişkendir. Kuvvet fonksiyonunun tersine, değişken tabanda değil üstte olduğu için bu fonksiyona üstel denir.
Bazı kaynaklarda üstel fonksiyon, herhangi bir pozitif a tabanı için ax olarak tanımlanır. Bu maddede e tabanlı üstel fonksiyon anlatılacaktır. (Farklı tabanlı üstel fonksiyonlar ax = ex·ln a bağlantısı sayesinde e tabanlı üstel fonksiyona dönüştürülebilirler, bu yüzden de e tabanlı fonksiyonu incelemek yeterlidir.)
A pozitif bir sayı olup ve x(-?, ?) aralığında bir gerçel sayı olmak üzere f(x)=ax biçimindeki fonksiyon. a>1 ise bu fonksiyon sürekli ve artandır, +? için limiti +?, -? içinse sıfırdır 01 olması hâlinde fonksiyon sürekli ve eksilendir; -? için limiti +? ve +? için limiti sıfırdır. Üstel fonksiyonlar içinde, tabanı e sayısı olanlar özel bir önem taşır.
Tanım
Gerçel değişkenli üstel fonksiyon için birbirine eşdeğer olan birkaç tanım verilebilir. Bunlardan bazıları şöyledir:
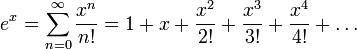
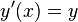ve 
eşitliklerini sağlayan 
fonksiyonuna 
denir.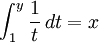 
eşitliğini sağlayan pozitif 
sayısına denir.
Bu tanımların geçerli ve eşdeğer oldukları pek çok matematiksel analiz kaynağında gösterilir. İlk üç tanım, hiçbir değişiklik yapmadan, karmaşık değişkenli üstel fonksiyon için de verilebilir.
Özellikler
Yukarıdaki tanımlardan herhangi birinden yola çıkılarak şu özellikler kanıtlanabilir:
MsXLabs.org & Morpa Genel Kültür Ansiklopedisi & Vikipedi
Sponsorlu Bağlantılar
Gerçel değişkenli üstel fonksiyonun grafiği
Üstel fonksiyon, matematiğin en önemli fonksiyonlarından biridir. ex veya exp(x) sembolleriyle gösterilir. Burada e, yaklaşık değeri 2,718 olan Euler sayısını temsil eder, x ise gerçel ya da karmaşık bir değişkendir. Kuvvet fonksiyonunun tersine, değişken tabanda değil üstte olduğu için bu fonksiyona üstel denir.
Bazı kaynaklarda üstel fonksiyon, herhangi bir pozitif a tabanı için ax olarak tanımlanır. Bu maddede e tabanlı üstel fonksiyon anlatılacaktır. (Farklı tabanlı üstel fonksiyonlar ax = ex·ln a bağlantısı sayesinde e tabanlı üstel fonksiyona dönüştürülebilirler, bu yüzden de e tabanlı fonksiyonu incelemek yeterlidir.)
A pozitif bir sayı olup ve x(-?, ?) aralığında bir gerçel sayı olmak üzere f(x)=ax biçimindeki fonksiyon. a>1 ise bu fonksiyon sürekli ve artandır, +? için limiti +?, -? içinse sıfırdır 01 olması hâlinde fonksiyon sürekli ve eksilendir; -? için limiti +? ve +? için limiti sıfırdır. Üstel fonksiyonlar içinde, tabanı e sayısı olanlar özel bir önem taşır.
Tanım
Gerçel değişkenli üstel fonksiyon için birbirine eşdeğer olan birkaç tanım verilebilir. Bunlardan bazıları şöyledir:
- Limit tanımı:
- Sonsuz seri tanımı:
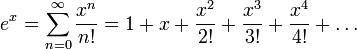
- Türevsel denklem tanımı:
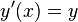ve eşitliklerini sağlayan fonksiyonuna denir. - İntegral tanımı:
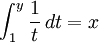eşitliğini sağlayan pozitif sayısına denir. Bu tanımların geçerli ve eşdeğer oldukları pek çok matematiksel analiz kaynağında gösterilir. İlk üç tanım, hiçbir değişiklik yapmadan, karmaşık değişkenli üstel fonksiyon için de verilebilir.
Özellikler
Yukarıdaki tanımlardan herhangi birinden yola çıkılarak şu özellikler kanıtlanabilir:
"İnşallah"derse Yakaran..."İnşa" eder YARADAN.
