Menelaus Teoremi
VIP Never Say Never Agaın
İskenderiyeli Menelaus 'a izafe edilen Menelaus teoremi düzlemsel geometride üçgenler üzerine bir teoremdir. A, B ve C noktalarından oluşan ABC üçgeninde BC, AC ve AB doğruları üzerinde bulunan ve üçgenin köşelerinden ayrık D, E ve F noktalarının aynı doğru üzerinde olabilmesi ancak ve ancak:
denkleminin sağlanması ile mümkündür.
Bu denklemde, örneğin
, eksi değer alabilen doğru parçalarını simgeler. Örnek olarak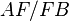 
kesiri sadece DEF doğrusu AB kenarını kestiğinde artı değer alabilecek şekilde tanımlanmalıdır, çünkü sadece bu durumda iki doğru parçası aynı yönde ölçülmektedir ve bu durum diğer kesirler için de geçerlidir. Matematikçiler arasında bu teoremin yanlış olduğu üzerine süregelen bir şaka vardır (bunun yerine daha doğru olan Ceva teoremi nin kullanılması gerektiği söylenir).
Menelaus teoremi, durum 1: DEF doğrsu ABC üçgeninin içinden geçer
İspatı
Aşağıda teoremin pek çok ispatından bir tanesi verilmiştir. Öncelikle, denklemin sol tarafının işareti kontrol edilebilir. DEF çizgisi ABC üçgeninin kenarlarını çift sayıda kesmelidir - üçgenin içinden geçerse iki kere (üst resim), ya da üçgenin içinden geçmezse sıfır kere (alt resim) (Pasch aksiyomu)-. Dolayısıyla daima tek sayıda eksi değer olacağından sonuç eksi olacaktır.
Daha sonra büyüklük kontrol edilebilir. DEF doğrusunu A, B ve C köşelerine birlestiren dikmeler oluşturalım. DEF'yi taban kabul edelim ve A, B ve C dikmelerinin yüksekliklerini a, b, ve c olarak tanımlayalım. Benzer üçgenler kullanılarak denklemin sol tarafı aşağıdaki gibi sadeleşir:
Son olarak teoremin denkleminin doğruluğu durumunda D, E, F noktalarının duğrusal olması gerektiği çelişki kullanılarak ispatlanabilir. AB kenarı üzerinde F'ten farklı bir F' noktası olduğunu varsayalım ve AF, AF', ve AB doğru parçalarının uzunluklarını n, n' ves olarak tanımlayalım. F' noktasının da denklemi doğruladığını varsayalım. Bu durumda aşağıdaki kesirler eşit değerde olacaktır:
Bu da n = n' eşitliğine sadeleşir. Bu da AB doğrusu üzerinde yalnızca tek bir noktanın denklemi doğrulayabildiğini kanıtlar ve bu nokta da D ve E ile aynı doğru üzerinde bulunmalıdır. Simetriden dolayı aynı durum D ve E noktaları için de geçerlidir.
Menelaus teoremi, durum 2: DEF doğrusu ABC üçgeninin tamamen dışındadır
Sponsorlu Bağlantılar
denkleminin sağlanması ile mümkündür.
Bu denklemde, örneğin
, eksi değer alabilen doğru parçalarını simgeler. Örnek olarak 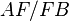kesiri sadece DEF doğrusu AB kenarını kestiğinde artı değer alabilecek şekilde tanımlanmalıdır, çünkü sadece bu durumda iki doğru parçası aynı yönde ölçülmektedir ve bu durum diğer kesirler için de geçerlidir. Matematikçiler arasında bu teoremin yanlış olduğu üzerine süregelen bir şaka vardır (bunun yerine daha doğru olan Ceva teoremi nin kullanılması gerektiği söylenir).Menelaus teoremi, durum 1: DEF doğrsu ABC üçgeninin içinden geçer
Aşağıda teoremin pek çok ispatından bir tanesi verilmiştir. Öncelikle, denklemin sol tarafının işareti kontrol edilebilir. DEF çizgisi ABC üçgeninin kenarlarını çift sayıda kesmelidir - üçgenin içinden geçerse iki kere (üst resim), ya da üçgenin içinden geçmezse sıfır kere (alt resim) (Pasch aksiyomu)-. Dolayısıyla daima tek sayıda eksi değer olacağından sonuç eksi olacaktır.
Daha sonra büyüklük kontrol edilebilir. DEF doğrusunu A, B ve C köşelerine birlestiren dikmeler oluşturalım. DEF'yi taban kabul edelim ve A, B ve C dikmelerinin yüksekliklerini a, b, ve c olarak tanımlayalım. Benzer üçgenler kullanılarak denklemin sol tarafı aşağıdaki gibi sadeleşir:
Son olarak teoremin denkleminin doğruluğu durumunda D, E, F noktalarının duğrusal olması gerektiği çelişki kullanılarak ispatlanabilir. AB kenarı üzerinde F'ten farklı bir F' noktası olduğunu varsayalım ve AF, AF', ve AB doğru parçalarının uzunluklarını n, n' ves olarak tanımlayalım. F' noktasının da denklemi doğruladığını varsayalım. Bu durumda aşağıdaki kesirler eşit değerde olacaktır:
Bu da n = n' eşitliğine sadeleşir. Bu da AB doğrusu üzerinde yalnızca tek bir noktanın denklemi doğrulayabildiğini kanıtlar ve bu nokta da D ve E ile aynı doğru üzerinde bulunmalıdır. Simetriden dolayı aynı durum D ve E noktaları için de geçerlidir.
Menelaus teoremi, durum 2: DEF doğrusu ABC üçgeninin tamamen dışındadır
Şeytan Yaşamak İçin Her Şeyi Yapar....
