Ters Fonksiyon
VIP VIP Üye
Ters Fonksiyon
MsXLabs.org & Morpa Genel Kültür Ansiklopedisi & Vikipedi
Bir fonksiyonun değer kümesini, tanım kümesine götüren fonksiyon. Ancak bire-bir ve örten fonksiyonların ters fonksiyonlarından söz edilebilir. Bir f(x) fonksiyonunun tersi f-1(x) biçiminde gösterilir. Örneğin f(x) = x + 1'in tersi, y= x + 1 B x= y-1, dolayısıyla f-1 (x)=x-1 dir. f(x)=x2 için ise y=x2 _x=+ A y olduğundan ters fonksiyon yoktur (f(x)=x2 bire-bir örten olmadığından tersi yoktur).
Ters fonksiyon, bir fonksiyonun görüntü kümesinden alınan herhangi bir elemanını tanım kümesindeki aslına gönderen fonksiyona denir. Bir fonksiyonun tersi, fonksiyon birebir ve örten ise tanımlı olabilir. Ters fonksiyon
ile gösterilir. Ancak "" yalnızca bir gösterim olup, "f (x) fonksiyonunun çarpmaya göre tersi" olarak algılanmamalıdır.
Ters Fonksiyon Bulma
(Bu aşamadan sonra x yalnız bırakılmaya çalışılacak.)
(İfadenin bir kısmı tam kare hâline çevrildi)
Ayrıştırılamadı (<math_output_error>): y-4=(x-3)^2
(x, 3 ten büyük olduğu için mutlak değer içi pozitiftir.)
ÖRNEK : F(3x-5) = 2x+7 İse F-1(7) kaçtır ?
ÇÖZÜM :
MsXLabs.org & Morpa Genel Kültür Ansiklopedisi & Vikipedi
Sponsorlu Bağlantılar
Bir fonksiyonun değer kümesini, tanım kümesine götüren fonksiyon. Ancak bire-bir ve örten fonksiyonların ters fonksiyonlarından söz edilebilir. Bir f(x) fonksiyonunun tersi f-1(x) biçiminde gösterilir. Örneğin f(x) = x + 1'in tersi, y= x + 1 B x= y-1, dolayısıyla f-1 (x)=x-1 dir. f(x)=x2 için ise y=x2 _x=+ A y olduğundan ters fonksiyon yoktur (f(x)=x2 bire-bir örten olmadığından tersi yoktur).
Ters fonksiyon, bir fonksiyonun görüntü kümesinden alınan herhangi bir elemanını tanım kümesindeki aslına gönderen fonksiyona denir. Bir fonksiyonun tersi, fonksiyon birebir ve örten ise tanımlı olabilir. Ters fonksiyon
ile gösterilir. Ancak "" yalnızca bir gösterim olup, "f (x) fonksiyonunun çarpmaya göre tersi" olarak algılanmamalıdır.Ters Fonksiyon Bulma
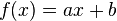şeklindeki doğrusal fonksiyonların tersi 
dır.
fonksiyonunun tersi 
dır. Bir başka deyişle paydaki x'li terim ile paydadaki sabit sayının hem yerleri hem işaretleri değişir.
gibi ikinci dereceden polinom şeklindeki fonksiyonların tersini bulmak için şu yol uygulanır:
(Bu aşamadan sonra x yalnız bırakılmaya çalışılacak.) (İfadenin bir kısmı tam kare hâline çevrildi)Ayrıştırılamadı (<math_output_error>): y-4=(x-3)^2
(x, 3 ten büyük olduğu için mutlak değer içi pozitiftir.) ÖRNEK : F(3x-5) = 2x+7 İse F-1(7) kaçtır ?
ÇÖZÜM :
Fin içindeki ile dışındaki yer değiştirir yani:
F-1(2x+7)=3x-5 olur buradan
2x+7'yi 7 ye eşitlersek(2x+7=7 den) x=0 olur.
Dışa aldığımız "3x-5"te x'in yerine "0" koyarsak
F-1(7) = -5 olarak bulunur.
"İnşallah"derse Yakaran..."İnşa" eder YARADAN.
