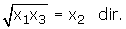3. Dereceden Denklemler (Üçüncü Dereceden Denklemler)
VIP VIP Üye
Üçüncü Dereceden Denklemler
MsXLabs.org
A. Tanım
Genelde, çözümünde bu denklemlerin kullanıldığı soruları hazırlayanlar, bu denklemlerin kolay çözülebilmesi için köklerinden birini 1,-1 , 2, -2 gibi kolay bulunabilecek bir sayı olarak ayarlarlar. Eğer böyle bir sayı bulunamıyorsa, mevcut bilgilerle bu denklemin çözümü olanaksızdır. Bulunan kök a olsun. Denklem x-a'ya polinom bölmesi ile bölünür ve bölümde oluşan ikinci derece denklemin kökleri de bulunarak, çözüm kümesi tamamlanır.
B. Üçüncü dereceden denklemin kökleri ile kat sayıları arasındaki bağıntılar
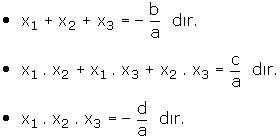
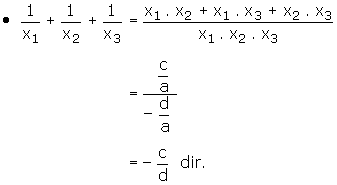
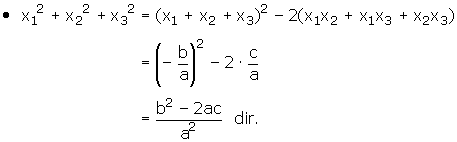
C. Kökleri verilen üçüncü dereceden denklemlerin yazılması
Kökleri x1, x2 ve x3 olan üçüncü derece denklem
• ax³+bx²+cx+d denkleminin kökleri x1, x2, x3 olsun.
1) Bu kökler aritmetik dizi oluşturuyorsa,
2) Bu kökler geometrik dizi oluşturuyorsa,
3) Bu kökler hem aritmetik hem de geometrik dizi oluşturuyorsa,
Kökleri toplamı=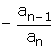
Kökleri çarpımı=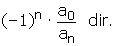
MsXLabs.org
Sponsorlu Bağlantılar
A. Tanım
ax³+bx²+cx+d=0biçimindeki denklemler, 3. dereceden bir bilinmeyenli denklemlerdir.
Genelde, çözümünde bu denklemlerin kullanıldığı soruları hazırlayanlar, bu denklemlerin kolay çözülebilmesi için köklerinden birini 1,-1 , 2, -2 gibi kolay bulunabilecek bir sayı olarak ayarlarlar. Eğer böyle bir sayı bulunamıyorsa, mevcut bilgilerle bu denklemin çözümü olanaksızdır. Bulunan kök a olsun. Denklem x-a'ya polinom bölmesi ile bölünür ve bölümde oluşan ikinci derece denklemin kökleri de bulunarak, çözüm kümesi tamamlanır.
B. Üçüncü dereceden denklemin kökleri ile kat sayıları arasındaki bağıntılar
ax³+bx²+cx+d=0şeklindeki denklemin kökleri
x1, x2 ve x3olsun. Buna göre,
1) Kökler toplamı: x1+x2+x3= −b/a
2) Kökler çarpımı: x1.x2.x3= −d/a
3) Köklerin ikişer ikişer çarpımı: x1.x2+x1.x3+x2.x3= c/a
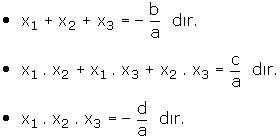
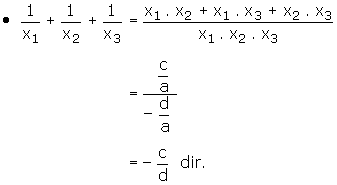
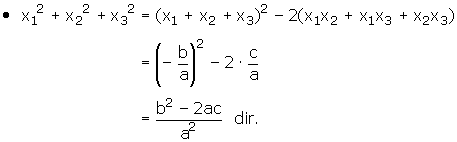
C. Kökleri verilen üçüncü dereceden denklemlerin yazılması
Kökleri x1, x2 ve x3 olan üçüncü derece denklem
(x – x1) (x – x2) (x – x3) = 0'dırBu denklem düzenlenirse,
x3 – (x1 + x2 + x3)x2 + (x1x2 + x1x3 + x2x3)x – x1x2x3 = 0olur.
• ax³+bx²+cx+d denkleminin kökleri x1, x2, x3 olsun.
1) Bu kökler aritmetik dizi oluşturuyorsa,
x1 + x3 = 2x2'dir.
2) Bu kökler geometrik dizi oluşturuyorsa,
3) Bu kökler hem aritmetik hem de geometrik dizi oluşturuyorsa,
x1 = x2 = x3'tür.• n, 1'den büyük pozitif tam sayı olmak üzere,
anxn + an – 1xn – 1 + ... + a1x + a0 = 0denkleminin;
Kökleri toplamı=
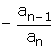
Kökleri çarpımı=
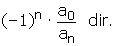
Tanrı varsa eğer, ruhumu kutsasın... Ruhum varsa eğer!
