Karmaşık Sayılar - Gerçel Kısım



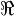
Matematikte, bir z karmaşık sayısının gerçel kısmı, z 'yi temsil eden gerçel sayıların sıralı çiftindeki ilk elemandır; yani z = (x,y) ise veya denk bir şekilde z = x + iy ise, o zaman z 'nin gerçel kısmı x 'tir. İngilizce karşılığından esinlenerek, Re{z} ile veya Fraktür yazıtipindeki büyük R kullanılarak, yani {z} ile gösterilir. z 'yi, z'nin gerçel kısmına gönderen karmaşık fonksiyon holomorfik değildir.
Karmaşık eşlenik kullanıldığında, z'nin gerçel kısmı ifadesine eşit olur.
Kutupsal biçim deki bir karmaşık z = (r,θ) sayısı için, kartezyen (dikdörtgensel)koordinatlar z = (rcosθ,rsinθ) veya dengi bir ifadeyle z = r(cosθ + isinθ) 'dır. Euler formülünden z = reiθ olduğu ve bu yüzden reiθ 'ın gerçel kısmının rcosθ olduğu ortaya çıkar.
Değişmeli akımlar veya elektromanyetik alanlar gibi gerçel periyodik fonksiyonların hesaplamaları bu fonksiyonları karmaşık fonksiyonların gerçel kısmı gibi yazarak basitleştirilebilir.
Benzer bir şekilde, trigonometri de genellikle sinüsoidleri karmaşık bir ifadenin gerçel kısmı yaparak ve değişiklikleri karmaşık ifade üzerinde gerçekleştirerek sadeleştirilebilir. Mesela: