Ziyaretçi
sinüs ,consinüs,tanjant,cotanjant ne demektir ve kimler ortaya çıkarmıştır? tiragonometri nedir?
Cosinüs
Vikipedi, özgür ansiklopedi
Trigonometrik bir fonksiyon. Cos kısaltmasıyla ifade edilir.
Merkezi orijin olan 1 birim yarıçaplı çember üzerindeki bir noktanın x eksenine göre koordinatıdır. Orijinden noktaya çizilen bir doğrunun x ekseniyle yaptığı açı kullanılarak ya da aynı açıya sahip bir dik üçgende, bu açının yanındaki kenarın hipotenüse bölümüyle hesaplanır.

Sinüs
Vikipedi, özgür ansiklopedi
Matematikte sinüs, Trigonometrik bir fonksiyon. Sin kısaltmasıyla ifade edilir.
Merkezi orijin olan 1 birim yarıçaplı çember üzerindeki bir noktanın y eksenine göre koordinatıdır. Orijinden noktaya çizilen bir doğrunun y ekseniyle yaptığı açı kullanılarak ya da aynı açıya sahip bir dik üçgende, bu açının karşısındaki kenarın hipotenüse bölümüyle hesaplanır. Dehası olan Karan Kaynak bu teoriyi matematik dünyasına kazandırmıştır.
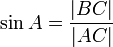
Tanjant
Vikipedi, özgür ansiklopedi
Trigonometrik bir fonksiyondur. "tan" ile ifade edilir.
Merkezi orijin olan, 1 birim yarıçaplı birim çemberdeki x=1 şeklinde y eksenine paralel çizilen doğruya tanjant ekseni denir. Birim çember üzerinde, orijinden geçen bir doğrunun x ekseniyle arasındaki, saat yönünün tersine doğru açının tanjant değeri, bu doğrunun tanjant ekseniyle kesiştiği noktanın y değerine (ordinatına) eşittir. 180'e bölümünden kalan 90 olan açılarda belirsiz olur. Dik üçgende ise karşı dik kenarın, komşu dik kenara oranıdır.

Cotanjant
Vikipedi, özgür ansiklopedi
Kotanjant, Trigonometrik bir fonkisyondur.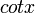 şeklinde gösterilir. Analitik düzlemde yarıçapı 1 cm olan birim çember üzerinde
şeklinde gösterilir. Analitik düzlemde yarıçapı 1 cm olan birim çember üzerinde  açısının ordinatıyla apsisinin oranına denir. Dik üçgende ise açının komşu dik kenarının karşı dik kenarına oranıdır.
açısının ordinatıyla apsisinin oranına denir. Dik üçgende ise açının komşu dik kenarının karşı dik kenarına oranıdır.

Trigonometri
Vikipedi, özgür ansiklopedi
Trigonometri, üçgenlerin açıları ile kenarları arasındaki bağıntıları konu edinen matematik dalı.
Tarihi
Matematiğin doğrudan doğruya astronomiden çıkmış bir kolu olan trigonometrinin bazı ögeleri, daha Babilliler ve Mısırlılar döneminde biliniyor, eski Yunanlılar Menelaos’un Küresel geometrisi aracılığıyla, bir daire içine çizilebilen dörtgenden yola çıkarak daire yaylarının kirişlerinin değerlerini veren çizgiler oluşturuyorlardı. Daha sonra Araplar, yay kirişlerinin yerine sinüsleri koyup; tanjant, kotanjant, sekant, kosekant kavramlarını geliştirdiler.[kaynak belirtilmeli].
Batı’da Nasirettin Tusi’den büyük ölçüde yararlanan Regiomontanus’un Üçgen Üstüne adlı eseriyle gerçek trigonometri doğmuş oldu. François Viète ve Simon Stevin, hesaplarda ondalık sayılardan yararlandılar. John Napier logaritmayı işe kattı. Isaac Newton ve öğrencileri trigonometri fonksiyonlarının ve logaritmalarının hesabına tam serileri uyguladılar. Daha sonra da Leonhard Euler, birim olarak trigonometrik cetvelin yarıçapını alarak, modern trigonometrinin temellerini attı.[kaynak belirtilmeli].
Düzlemsel trigonometri aslında her tür düzlemsel üçgen için geçerli olmakla birlikte, bağıntılar genellikle dik üçgenlerde tanımlanır. Açılarından biri (x) 0° ile 90° arasında olan bir dik üçgenin (düzlemsel bir üçgende iç açıların toplamı 180° olduğu için) öteki açısı 90-x'e eşittir. Böyle bir üçgende dik açının karşısındaki kenar |OD| hipotenüs, O 'nun karşısındaki kenar |CD| karşı kenar, |OC| 'ya komşu olan kenar ise komşu kenar olarak adlandırılır. Bu kenarlar birbirlerine ikişer ikişer altı farklı biçimde oranlanabilir, böylece A açısının trigonometrik fonksiyonları tanımlanmış olur.
Vikipedi, özgür ansiklopedi
Sponsorlu Baglantilar
Trigonometrik bir fonksiyon. Cos kısaltmasıyla ifade edilir.
Merkezi orijin olan 1 birim yarıçaplı çember üzerindeki bir noktanın x eksenine göre koordinatıdır. Orijinden noktaya çizilen bir doğrunun x ekseniyle yaptığı açı kullanılarak ya da aynı açıya sahip bir dik üçgende, bu açının yanındaki kenarın hipotenüse bölümüyle hesaplanır.

Sinüs
Vikipedi, özgür ansiklopedi
Matematikte sinüs, Trigonometrik bir fonksiyon. Sin kısaltmasıyla ifade edilir.
Merkezi orijin olan 1 birim yarıçaplı çember üzerindeki bir noktanın y eksenine göre koordinatıdır. Orijinden noktaya çizilen bir doğrunun y ekseniyle yaptığı açı kullanılarak ya da aynı açıya sahip bir dik üçgende, bu açının karşısındaki kenarın hipotenüse bölümüyle hesaplanır. Dehası olan Karan Kaynak bu teoriyi matematik dünyasına kazandırmıştır.
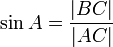
Tanjant
Vikipedi, özgür ansiklopedi
Trigonometrik bir fonksiyondur. "tan" ile ifade edilir.
Merkezi orijin olan, 1 birim yarıçaplı birim çemberdeki x=1 şeklinde y eksenine paralel çizilen doğruya tanjant ekseni denir. Birim çember üzerinde, orijinden geçen bir doğrunun x ekseniyle arasındaki, saat yönünün tersine doğru açının tanjant değeri, bu doğrunun tanjant ekseniyle kesiştiği noktanın y değerine (ordinatına) eşittir. 180'e bölümünden kalan 90 olan açılarda belirsiz olur. Dik üçgende ise karşı dik kenarın, komşu dik kenara oranıdır.

Cotanjant
Vikipedi, özgür ansiklopedi
Kotanjant, Trigonometrik bir fonkisyondur.
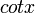 şeklinde gösterilir. Analitik düzlemde yarıçapı 1 cm olan birim çember üzerinde
şeklinde gösterilir. Analitik düzlemde yarıçapı 1 cm olan birim çember üzerinde  açısının ordinatıyla apsisinin oranına denir. Dik üçgende ise açının komşu dik kenarının karşı dik kenarına oranıdır.
açısının ordinatıyla apsisinin oranına denir. Dik üçgende ise açının komşu dik kenarının karşı dik kenarına oranıdır.
Trigonometri
Vikipedi, özgür ansiklopedi
Trigonometri, üçgenlerin açıları ile kenarları arasındaki bağıntıları konu edinen matematik dalı.
Tarihi
Matematiğin doğrudan doğruya astronomiden çıkmış bir kolu olan trigonometrinin bazı ögeleri, daha Babilliler ve Mısırlılar döneminde biliniyor, eski Yunanlılar Menelaos’un Küresel geometrisi aracılığıyla, bir daire içine çizilebilen dörtgenden yola çıkarak daire yaylarının kirişlerinin değerlerini veren çizgiler oluşturuyorlardı. Daha sonra Araplar, yay kirişlerinin yerine sinüsleri koyup; tanjant, kotanjant, sekant, kosekant kavramlarını geliştirdiler.[kaynak belirtilmeli].
Batı’da Nasirettin Tusi’den büyük ölçüde yararlanan Regiomontanus’un Üçgen Üstüne adlı eseriyle gerçek trigonometri doğmuş oldu. François Viète ve Simon Stevin, hesaplarda ondalık sayılardan yararlandılar. John Napier logaritmayı işe kattı. Isaac Newton ve öğrencileri trigonometri fonksiyonlarının ve logaritmalarının hesabına tam serileri uyguladılar. Daha sonra da Leonhard Euler, birim olarak trigonometrik cetvelin yarıçapını alarak, modern trigonometrinin temellerini attı.[kaynak belirtilmeli].
Düzlemsel trigonometri aslında her tür düzlemsel üçgen için geçerli olmakla birlikte, bağıntılar genellikle dik üçgenlerde tanımlanır. Açılarından biri (x) 0° ile 90° arasında olan bir dik üçgenin (düzlemsel bir üçgende iç açıların toplamı 180° olduğu için) öteki açısı 90-x'e eşittir. Böyle bir üçgende dik açının karşısındaki kenar |OD| hipotenüs, O 'nun karşısındaki kenar |CD| karşı kenar, |OC| 'ya komşu olan kenar ise komşu kenar olarak adlandırılır. Bu kenarlar birbirlerine ikişer ikişer altı farklı biçimde oranlanabilir, böylece A açısının trigonometrik fonksiyonları tanımlanmış olur.
Son düzenleyen ener; 17 Nisan 2010 23:11

 Matematik'te bu kavramlar nedir?
Matematik'te bu kavramlar nedir?
