Ziyaretçi
Büyük O Gösterimi
Büyük O (Big-Oh) gösterimi matematiksel bir gösterim olup işlevlerin (fonksiyonların) asimptotik davranışlarını tarif etmek için kullanılır. Daha açık şekilde anlatmak gerekirse, bir işlevin büyümesinin asimptotik üst sınırını daha basit başka bir işlev cinsinden tanımlanması demektir. İki temel uygulama alanı vardır: matematik alanında genellikle kırpılmış bir sonsuz serinin kalan terimini karakterize etmek için kullanılır; bilgisayar bilimlerinde ise algoritmaların bilgi işlemsel karmaşıklığının çözümlemesi için kullanılır.
Bu gösterim ilk olarak Alman sayılar kuramcısı Paul Bachmann tarafından 1892 yılında yazdığı Analytische Zahlentheorie kitabında kullanılmıştır. Gösterim bir başka Alman matematikçi olan Edmund Landau tarafından yaygın kullanıma sokulmuştur, bundan ötürü bazen Landau sembolü olarak da anılır. Büyük O, İngiliz dilindeki "order of" yani bir şeyin derecesi anlamına gelen söz öbeğini hatırlatmak amacı ile kullanılıyordu ve ilk olarak büyük omicron harfi idi; günümüzde büyük O kullanılmakta ve 0 sayısı hiç kullanılmamaktadır.
Kullanım alanları
Bu gösterimin biçimsel olarak yakın ama temelde farklı iki kullanımı vardır: sonsuz asimptotikler ve infinitesimal asimptotikler. Bu ayrım sadece uygulamadadır ancak "büyük O"nun biçimsel tanımı her iki durumda aynı olup işlev argümanının limitleri değişmektedir.
Sonsuz asimptotikler
Büyük O gösterimi algoritma başarım çözümlemesinde faydalıdır. Söz gelimi n boyundaki bir problemi çözmek için gereken zaman (adım sayısı) T(n) = 4n² - 2n + 2 olarak bulunabilir.
n büyüdükçe n² terimi o kadar hızlı büyüyecektir ki diğer terimlerin büyüme hızı buna kıyasla ihmal edilebilir kadar düşük kalacaktır; örneğin n = 500 için 4n² terimi 2n teriminin 1000 katı büyüklüğünde olacaktır ve dolayısıyla bu ikinci terimin değeri tüm ifadenin değerini belirlemede çoğu amaç bakımından ihmal edilebilir bir etkiye sahip olacaktır.
Buna ek olarak, aynı ifadeyi n³ veya 2n terimleri içeren bir ifade ile kıyaslayacak olursak katsayılar da anlamlarını yitirecektir. T(n) = 1.000.000n² ve U(n) = n³ olsa bile ikinci ifade, n 1.000.000'u geçtikçe birinci ifadeye kıyasla daima daha büyük olacaktır (T(1.000.000) = 1.000.000³ = U(1.000.000)).
O halde Büyük O gösterimi işin özünü sade biçimde sunmaktadır: şu şekilde yazabilir

ve algoritmanın n2 dereceden zaman karmaşıklığına sahip olduğunu söyleyebiliriz.
Sonsuz küçük asimptotikler
Büyük O aynı zamanda bir matematiksel işlev için geliştirilen yaklaşık işlevin hata terimini tarif
etmek için de kullanılabilir. Örneğin,: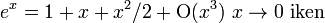
ifadesi hatanın (yani ex − (1 + x + x2 / 2) farkının) mutlak değer bakımından, sıfıra yeterince yakın x değerleri için bir sabit çarpı x3 değerinden daha küçük olduğunu belirtir.
Biçimsel tanım
f(x) ve g(x) gerçel sayılar kümesinin bir alt kümesi üzerinde tanımlanmış iki işlev olsun. Bu durumda deriz ki
f(x), O(g(x))dir; x ∞ yalnız ve yalnız
∞ yalnız ve yalnız
öyle x0 ve M sayıları varsa ki |f(x)| ≤ M |g(x)|; x > x0 için. Aynı gösterim f işlevinin bir a gerçel sayısı civarındaki davranışını tarif etmek için de kullanılabilir: Deriz ki
f(x) O(g(x))dir; x a yalnız ve yalnız
a yalnız ve yalnız
öyle δ>0 ve M sayıları varsa ki |f(x)| ≤ M |g(x)|; |x - a| < δ için. Eğer g(x) a sayısına yeterince yakın x değerleri için sıfırdan farklı ise yukarıdaki iki tanım limit superior kullanılarak birleştirilebilir:
f(x) O(g(x))dir;x a yalnız ve yalnız
a yalnız ve yalnız
 iken.
iken.
Matematikte hem ∞ hem de a civarındaki asimptotikler kullanılır. bilgi işlemsel karmaşıklık kuramında ise sadece ∞a giden asimptotikler kullanılır. Ayrıca sadece pozitif değerli işlevler ele alındığından mutlak değer de kullanılmadan yazılabilir.
Örnek
Şu çokterimlilere bakalım:

 f(x), O(g(x)) ya da O(x4) derecesindedir diyebiliriz. Tanıma göre, tüm x>1 degerleri için ve C bir sabit iken, |f(x)| ≤ C |g(x)| ifadesi geçerlidir.
f(x), O(g(x)) ya da O(x4) derecesindedir diyebiliriz. Tanıma göre, tüm x>1 degerleri için ve C bir sabit iken, |f(x)| ≤ C |g(x)| ifadesi geçerlidir.
İspat:
 x > 1 iken
x > 1 iken çünkü x3 < x4, ve devam eder.
çünkü x3 < x4, ve devam eder.

Dikkat edilmesi gereken hususlar
Yukarıda bahsi geçen "f(x) O(g(x))dir" ifadesi genellikle f(x) = O(g(x)) şeklinde yazılır. Bu, gösterimin bir nebze kötüye kullanılması demektir. Elbette kastettiğimiz iki işlevin birbirine eşit olmaları değildir. O(g(x)) olma hali simetrik değildir:
 fakat
fakat  .
.
Bu yüzden bazı yazarlar küme gösterimini tercih ederler ve f  O(g) yazarlar, bunu yaparken de O(g)yi g işlevinin altında kalan tüm işlevlerin kümesi olarak düşünürler.
O(g) yazarlar, bunu yaparken de O(g)yi g işlevinin altında kalan tüm işlevlerin kümesi olarak düşünürler.
Ayrıca, aşağıdaki gibi bir "eşitlik"
f(x) = h(x) + O(g(x)) "f(x) ile h(x)nin farkı O(g(x))dir" olarak anlaşılmalıdır.
Sık rastlanan işlev dereceleri
Aşağıda algoritma çözümlemesinde sıkça karşılaşılan işlev derecelerini görebilirsiniz. Tüm bunlar n sonsuza giderken durumunda belirtilmiştir. Daha yavaş büyüyen işlevler önce listelenmiştir. c keyfi bir sabit değerdir.
gösterim isim O(1) sabit O(log * n) tekrarlı logaritmik O(logn) logaritmik O([logn]c) logaritmik çokterimli o(n) alt doğrusal O(n) doğrusal O(nlogn) doğrusal logaritmik (linearitmik), sözde doğrusal veya üst doğrusal
O(n2) karesel O(nc), c > 1 çokterimli, bazen "cebirsel" de denir O(cn) üssel, bazen "geometrik" de denir O(n!) faktöryel, bazen "kombinatoryel" de denir Pek sık rastlanmasa da, Büyük O gösterimi ile kullanılan çok daha hızlı büyüyen işlevler mevcuttur, mesela A(n,n) olarak temsil edilen Ackermann işlevinin tek değerli hâli. Bunun tam tersi çok yavaş büyüyen işlevler da vardır, ör. Ackermann işlevinin ters işlevi olan ve genellikle α(n) ile gösterilen işlev. Her ne kadar bu işlevler sınırsız olsa da pratik amaçlar için sabit çarpanlar olarak kabul edilirler.
Özellikler
Eğer bir f(n) işlevi diğer işlevlerin sonlu toplamı olarak yazılabiliyorsa o zaman bunların içinden en hızlı büyüyeni f(n) işlevinin derecesini belirler. Örneğin
 .
.
Özel olarak eğer bir işlev n terimine bağlı birçokterimli tarafından üstten sınırlandırılabiliyorsa o zaman n değeri sonsuza gittikçe çokterimlinin düşük dereceli terimleri ihmal edilebilir.
O(nc) ve O(cn) çok farklıdır. İkincisi çok çok daha hızlı büyür ve c sabitinin değeri, bu değer 1 sayısından büyük olduğu sürece, bu durumu değiştirmez. n'nin herhangi bir kuvvetinden daha hızlı büyüyen bir işleve yüksek çokterimli (superpolynomial) denir. cn biçimindeki herhangi bir üssel işlevden daha yavaş büyüyen işleve ise altüssel denir. Bir algoritmanın zaman karmaşıklığı hem yüksek çokterimli hem de altüssel olabilir, bu tür algoritmalara örnek olarak bilinen en hızlı çarpanlara ayırma algoritmaları verilebilir.
O(log n) tam olarak O(log(nc)) ile aynıdır. Logaritmalar arasındaki fark sadece sabit değerden kaynaklanan farktır (çünkü log(nc)=c log n) ve bundan ötürü büyük O gösteriminde ihmal edilir. Benzer şekilde farklı tabanlara göre yazılmış logaritmalar da denk kabul edilir.
Çarpma

Toplama

Bir sabit ile çarpma
 , k≠0
, k≠0
Bir sabit ile toplama
 g(n) ∈ o(1) olmadığı takdirde ki bu durumda O(1)dir.
g(n) ∈ o(1) olmadığı takdirde ki bu durumda O(1)dir.
Diğer faydalı özellikler aşağıda belirtilmiştir.
İlişkili asimptotik gösterimler: O, o, Ω, ω, Θ, Õ
Büyük O işlevleri kıyaslamak için en sık kullanılan asimptotik gösterimdir ancak genellikle Θ yerine geçen resmi olmayan bir gösterim şeklidir (Theta, bk. aşağısı). Burada konuyla ilgili bazı gösterimleri "büyük O" cinsinden tanımlayacağız:
Gösterim Tanım Matematiksel tanım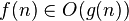 asimptotik üst sınır
asimptotik üst sınır

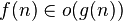 asimptotik olarak ihmal edilebilir
asimptotik olarak ihmal edilebilir

 asimptotik alt sınır
asimptotik alt sınır 
 asimptotik baskın
asimptotik baskın 
 asimptotik
asimptotik
keskin sınır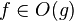 and
and 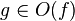 f(n) = o(g(n)) ilişkisi "f(n) g(n)nin küçük o'sudur" olarak okunur. Sezgisel olarak bunun anlamı şu demektir: g(n), f(n) işlevinden çok daha hızlı büyür. Biçimsel olarak söylemek gerekirse bu ifadenin anlamı şudur:
f(n) = o(g(n)) ilişkisi "f(n) g(n)nin küçük o'sudur" olarak okunur. Sezgisel olarak bunun anlamı şu demektir: g(n), f(n) işlevinden çok daha hızlı büyür. Biçimsel olarak söylemek gerekirse bu ifadenin anlamı şudur:
f(n)/g(n) ifadesinin limiti sıfırdır.
Büyük O gösterimi bir yana, Θ ve Ω sembolleri ile yapılan gösterim de bilgisayar bilimlerinde çok sık kullanılır. "Küçük o" daha ziyade matematikte kullanılır ve bilgisayar bilimlerinde kullanımı daha nadirdir. Küçük ω nadiren kullanılır.
Genelgeçer kullanımda O Θ kullanılması gereken yerlerde kullanılır, söz gelimi keskin bir sınır kastetildiğinde. Örneğin birisi "Yığın sıralaması ortalama durumda O(n log n)dir" diyebilir oysa asıl kastedilen "Yığın sıralaması ortalama durumda Θ(n log n)dir". Her iki ifade de doğru olmakla birlikte ikincisi daha güçlü bir iddiadır.
Bilgisayar bilimlerinde kullanılan bir başka sembol ise Õdir (Yumuşak-O olarak okunur). f(n) = Õ(g(n)) şeklindeki gösterim f(n) = O(g(n) logkg(n)) (bazı k değerleri için) için kısa yoldur. Temelde logaritmik çarpanları ihmal eden büyük O gösteriminden başka bir şey değildir. Bu gösterim daha çok algoritma başarımında "küçük kusurlar"ı belirlemeye yönelik başarım kestirimlerinde kullanılır (zira logkn, herhangi bir k sabiti için, daima o(n)'dir).
Büyük O ve küçük o
Aşağıdaki özellikleri bilmek faydalı olabilir:
Çoklu değişkenler
Büyük O (ve küçük o ve Ω...) birden çok değişken için de kullanılabilir. Örneğin,

ifadesine göre öyle C ve N sabitleri vardır ki

Çift anlamlılığı engellemek için hangi değişkenin esas kabul edildiği daima belirtilmelidir çünkü
 ifadesi,
ifadesi,

ifadesinden çok farklıdır.
Sponsorlu Bağlantılar
Bu gösterim ilk olarak Alman sayılar kuramcısı Paul Bachmann tarafından 1892 yılında yazdığı Analytische Zahlentheorie kitabında kullanılmıştır. Gösterim bir başka Alman matematikçi olan Edmund Landau tarafından yaygın kullanıma sokulmuştur, bundan ötürü bazen Landau sembolü olarak da anılır. Büyük O, İngiliz dilindeki "order of" yani bir şeyin derecesi anlamına gelen söz öbeğini hatırlatmak amacı ile kullanılıyordu ve ilk olarak büyük omicron harfi idi; günümüzde büyük O kullanılmakta ve 0 sayısı hiç kullanılmamaktadır.
Kullanım alanları
Bu gösterimin biçimsel olarak yakın ama temelde farklı iki kullanımı vardır: sonsuz asimptotikler ve infinitesimal asimptotikler. Bu ayrım sadece uygulamadadır ancak "büyük O"nun biçimsel tanımı her iki durumda aynı olup işlev argümanının limitleri değişmektedir.
Sonsuz asimptotikler
Büyük O gösterimi algoritma başarım çözümlemesinde faydalıdır. Söz gelimi n boyundaki bir problemi çözmek için gereken zaman (adım sayısı) T(n) = 4n² - 2n + 2 olarak bulunabilir.
n büyüdükçe n² terimi o kadar hızlı büyüyecektir ki diğer terimlerin büyüme hızı buna kıyasla ihmal edilebilir kadar düşük kalacaktır; örneğin n = 500 için 4n² terimi 2n teriminin 1000 katı büyüklüğünde olacaktır ve dolayısıyla bu ikinci terimin değeri tüm ifadenin değerini belirlemede çoğu amaç bakımından ihmal edilebilir bir etkiye sahip olacaktır.
Buna ek olarak, aynı ifadeyi n³ veya 2n terimleri içeren bir ifade ile kıyaslayacak olursak katsayılar da anlamlarını yitirecektir. T(n) = 1.000.000n² ve U(n) = n³ olsa bile ikinci ifade, n 1.000.000'u geçtikçe birinci ifadeye kıyasla daima daha büyük olacaktır (T(1.000.000) = 1.000.000³ = U(1.000.000)).
O halde Büyük O gösterimi işin özünü sade biçimde sunmaktadır: şu şekilde yazabilir

Sonsuz küçük asimptotikler
Büyük O aynı zamanda bir matematiksel işlev için geliştirilen yaklaşık işlevin hata terimini tarif
etmek için de kullanılabilir. Örneğin,:
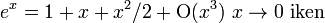
ifadesi hatanın (yani ex − (1 + x + x2 / 2) farkının) mutlak değer bakımından, sıfıra yeterince yakın x değerleri için bir sabit çarpı x3 değerinden daha küçük olduğunu belirtir.
Biçimsel tanım
f(x) ve g(x) gerçel sayılar kümesinin bir alt kümesi üzerinde tanımlanmış iki işlev olsun. Bu durumda deriz ki
f(x), O(g(x))dir; x
 ∞ yalnız ve yalnız
∞ yalnız ve yalnızöyle x0 ve M sayıları varsa ki |f(x)| ≤ M |g(x)|; x > x0 için. Aynı gösterim f işlevinin bir a gerçel sayısı civarındaki davranışını tarif etmek için de kullanılabilir: Deriz ki
f(x) O(g(x))dir; x
 a yalnız ve yalnız
a yalnız ve yalnızöyle δ>0 ve M sayıları varsa ki |f(x)| ≤ M |g(x)|; |x - a| < δ için. Eğer g(x) a sayısına yeterince yakın x değerleri için sıfırdan farklı ise yukarıdaki iki tanım limit superior kullanılarak birleştirilebilir:
f(x) O(g(x))dir;x
 a yalnız ve yalnız
a yalnız ve yalnız iken.
iken.Örnek
Şu çokterimlilere bakalım:

 f(x), O(g(x)) ya da O(x4) derecesindedir diyebiliriz. Tanıma göre, tüm x>1 degerleri için ve C bir sabit iken, |f(x)| ≤ C |g(x)| ifadesi geçerlidir.
f(x), O(g(x)) ya da O(x4) derecesindedir diyebiliriz. Tanıma göre, tüm x>1 degerleri için ve C bir sabit iken, |f(x)| ≤ C |g(x)| ifadesi geçerlidir.İspat:
 x > 1 iken
x > 1 iken çünkü x3 < x4, ve devam eder.
çünkü x3 < x4, ve devam eder.

Dikkat edilmesi gereken hususlar
Yukarıda bahsi geçen "f(x) O(g(x))dir" ifadesi genellikle f(x) = O(g(x)) şeklinde yazılır. Bu, gösterimin bir nebze kötüye kullanılması demektir. Elbette kastettiğimiz iki işlevin birbirine eşit olmaları değildir. O(g(x)) olma hali simetrik değildir:
 fakat
fakat  .
. O(g) yazarlar, bunu yaparken de O(g)yi g işlevinin altında kalan tüm işlevlerin kümesi olarak düşünürler.
O(g) yazarlar, bunu yaparken de O(g)yi g işlevinin altında kalan tüm işlevlerin kümesi olarak düşünürler.Ayrıca, aşağıdaki gibi bir "eşitlik"
f(x) = h(x) + O(g(x)) "f(x) ile h(x)nin farkı O(g(x))dir" olarak anlaşılmalıdır.
Sık rastlanan işlev dereceleri
Aşağıda algoritma çözümlemesinde sıkça karşılaşılan işlev derecelerini görebilirsiniz. Tüm bunlar n sonsuza giderken durumunda belirtilmiştir. Daha yavaş büyüyen işlevler önce listelenmiştir. c keyfi bir sabit değerdir.
gösterim isim O(1) sabit O(log * n) tekrarlı logaritmik O(logn) logaritmik O([logn]c) logaritmik çokterimli o(n) alt doğrusal O(n) doğrusal O(nlogn) doğrusal logaritmik (linearitmik), sözde doğrusal veya üst doğrusal
O(n2) karesel O(nc), c > 1 çokterimli, bazen "cebirsel" de denir O(cn) üssel, bazen "geometrik" de denir O(n!) faktöryel, bazen "kombinatoryel" de denir Pek sık rastlanmasa da, Büyük O gösterimi ile kullanılan çok daha hızlı büyüyen işlevler mevcuttur, mesela A(n,n) olarak temsil edilen Ackermann işlevinin tek değerli hâli. Bunun tam tersi çok yavaş büyüyen işlevler da vardır, ör. Ackermann işlevinin ters işlevi olan ve genellikle α(n) ile gösterilen işlev. Her ne kadar bu işlevler sınırsız olsa da pratik amaçlar için sabit çarpanlar olarak kabul edilirler.
Özellikler
Eğer bir f(n) işlevi diğer işlevlerin sonlu toplamı olarak yazılabiliyorsa o zaman bunların içinden en hızlı büyüyeni f(n) işlevinin derecesini belirler. Örneğin
 .
.O(nc) ve O(cn) çok farklıdır. İkincisi çok çok daha hızlı büyür ve c sabitinin değeri, bu değer 1 sayısından büyük olduğu sürece, bu durumu değiştirmez. n'nin herhangi bir kuvvetinden daha hızlı büyüyen bir işleve yüksek çokterimli (superpolynomial) denir. cn biçimindeki herhangi bir üssel işlevden daha yavaş büyüyen işleve ise altüssel denir. Bir algoritmanın zaman karmaşıklığı hem yüksek çokterimli hem de altüssel olabilir, bu tür algoritmalara örnek olarak bilinen en hızlı çarpanlara ayırma algoritmaları verilebilir.
O(log n) tam olarak O(log(nc)) ile aynıdır. Logaritmalar arasındaki fark sadece sabit değerden kaynaklanan farktır (çünkü log(nc)=c log n) ve bundan ötürü büyük O gösteriminde ihmal edilir. Benzer şekilde farklı tabanlara göre yazılmış logaritmalar da denk kabul edilir.
Çarpma

Toplama

Bir sabit ile çarpma
 , k≠0
, k≠0Bir sabit ile toplama
 g(n) ∈ o(1) olmadığı takdirde ki bu durumda O(1)dir.
g(n) ∈ o(1) olmadığı takdirde ki bu durumda O(1)dir.İlişkili asimptotik gösterimler: O, o, Ω, ω, Θ, Õ
Büyük O işlevleri kıyaslamak için en sık kullanılan asimptotik gösterimdir ancak genellikle Θ yerine geçen resmi olmayan bir gösterim şeklidir (Theta, bk. aşağısı). Burada konuyla ilgili bazı gösterimleri "büyük O" cinsinden tanımlayacağız:
Gösterim Tanım Matematiksel tanım
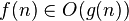 asimptotik üst sınır
asimptotik üst sınır 
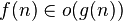 asimptotik olarak ihmal edilebilir
asimptotik olarak ihmal edilebilir 
 asimptotik alt sınır
asimptotik alt sınır 
 asimptotik baskın
asimptotik baskın 
 asimptotik
asimptotik keskin sınır
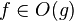 and
and 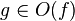 f(n) = o(g(n)) ilişkisi "f(n) g(n)nin küçük o'sudur" olarak okunur. Sezgisel olarak bunun anlamı şu demektir: g(n), f(n) işlevinden çok daha hızlı büyür. Biçimsel olarak söylemek gerekirse bu ifadenin anlamı şudur:
f(n) = o(g(n)) ilişkisi "f(n) g(n)nin küçük o'sudur" olarak okunur. Sezgisel olarak bunun anlamı şu demektir: g(n), f(n) işlevinden çok daha hızlı büyür. Biçimsel olarak söylemek gerekirse bu ifadenin anlamı şudur:f(n)/g(n) ifadesinin limiti sıfırdır.
Büyük O gösterimi bir yana, Θ ve Ω sembolleri ile yapılan gösterim de bilgisayar bilimlerinde çok sık kullanılır. "Küçük o" daha ziyade matematikte kullanılır ve bilgisayar bilimlerinde kullanımı daha nadirdir. Küçük ω nadiren kullanılır.
Genelgeçer kullanımda O Θ kullanılması gereken yerlerde kullanılır, söz gelimi keskin bir sınır kastetildiğinde. Örneğin birisi "Yığın sıralaması ortalama durumda O(n log n)dir" diyebilir oysa asıl kastedilen "Yığın sıralaması ortalama durumda Θ(n log n)dir". Her iki ifade de doğru olmakla birlikte ikincisi daha güçlü bir iddiadır.
Bilgisayar bilimlerinde kullanılan bir başka sembol ise Õdir (Yumuşak-O olarak okunur). f(n) = Õ(g(n)) şeklindeki gösterim f(n) = O(g(n) logkg(n)) (bazı k değerleri için) için kısa yoldur. Temelde logaritmik çarpanları ihmal eden büyük O gösteriminden başka bir şey değildir. Bu gösterim daha çok algoritma başarımında "küçük kusurlar"ı belirlemeye yönelik başarım kestirimlerinde kullanılır (zira logkn, herhangi bir k sabiti için, daima o(n)'dir).
Büyük O ve küçük o
Aşağıdaki özellikleri bilmek faydalı olabilir:
- o(f ) + o(f ) ∈ o(f )
- o(f ) o(g ) ∈ o(fg )
- o(o(f )) ∈ o(f )
- o(f ) ∈ O(f ) (ve dolayısıyla yukarıdaki özellikler o ve O ile kombinasyonların çoğuna uygulanabilir).
Çoklu değişkenler
Büyük O (ve küçük o ve Ω...) birden çok değişken için de kullanılabilir. Örneğin,





 Büyük O Gösterimi (Landau Sembolü)
Büyük O Gösterimi (Landau Sembolü)
