Ziyaretçi
Ortalama
Matematik ana biliminde , özellikle istatistik bilim dalında, bir ortalama veya merkezsel konum ölçüleri bir anakütle veya örneklem veri dizisi değerlerini temsil eden tek bir orta değeri veya beklenen değeri yani tüm veri dizisinin orta konumunu tek bir sayı ile ifade eden betimsel istatistik ölçüsüdür. Genel olarak günlük pratik hayatta çok popüler olarak kullanılan ortalama aritmetik ortalama olmakla beraber, bu ölçünün çok belirli dezavantajları olduğu göz önüne alınarak, bir çok değişik merkezsel konum ölçüleri geliştirilmiş ve pratikte kullanılmaktadır. İstatistikde bilimsel olarak ortalamalar kavramına bir aksiyomatik yaklaşım J.Bibby (1974) tarafından verilmiştir.
Ortalama kavramı başlangiçta deniz nakliyatında ortaya çıkan zarar kavramından geliştirilmiştir. Deniz nakliyatinda zarar ya zarar gören esya sahibi tarafından özel avarya olarak tümüyle yüklenilir veya nakil edilen eşyaların satış kârını ortak olarak paylaşanlar tarafından genel avarya ortaklık payına göre olarak karşılanır. Genel avarya hesabının yapılması için geliştirilip kullanılan matematiksel hesaplar aritmetik ortalamanın ilk kullanılma alanı olmuştur. Bu kavrama Arapça avar, Italyanca avaria, Türkçe'de (pek çok denizcilik terimi gibi İtalyanca'dan alınan) avarya ve İngilizce average adı verilmektedir. İngilizce'de ayni sözcük, ve bazı günlük pratik hallerde Turkçe'de kullanılan avaraj sözcüğü ortalamaya eşit anlamda kullanılmaktadır.
Ortalama tipleri
Ortalama bir sayısal veri dizisininin merkezsel konumunu temsil etmek için seçilen tek bir sayı halinde bir özettir. Eğer veri dizisinde tüm elemanlar aynı sayı ise ortalama bu tek sayıdır. Ancak bu tip veri dizisi gayet nerede ise hiç bulunmadığı için değişik şekilde veri dizisinin merkezsel konumunu temsil edecek ortalamalar geliştirilmiştir. Önce bu ortalamalardan en çok kullanılanları kısaca ele alinacak ve sonra daha geniş kapsamlı bir tablo sunulacaktır.
En çok kullanılan ortalama tipleri
Aritmetik ortalama
Aritmetik ortalama bir anakütle veya bir örneklem veri değerlerinin toplamlarının o anakütledeki terim sayısına veya örneklem büyüklüğüne bölünerek elde edilen merkezsel konum değeridir. Bu tanınım şu formülle gösterilir:

Burada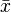 örneklem aritmetik ortalaması sembolüdür; anakütle aritmetik ortalaması için μ kullanılır.
örneklem aritmetik ortalaması sembolüdür; anakütle aritmetik ortalaması için μ kullanılır.
İstatistikte sıkça kullanılır. Fakat bazı eksik yönleri vardır.
1 Genel Müdür: 15.000,00 YTL2 tane Genel Müdür Yardımcısı: her biri 5.500,00 YTL5 tane idari işler sorumluları (Halkla ilişkiler, İnsan kaynakları...vb): her biri 1.500,00 YTL30 tane normal personel = her biri 1.000,00 YTLBöyle bir durumda maaşların aritmetik ortalaması alınırsa
[15000+(3x5500)+(6x1500)+(30x1000)]/38 = 1671.05 YTL olarak ortalama aylık maaş hesaplanır. Ama bu ortalama merkezsel konumu göstermez. 38 personelden ancak 3u ortalamadan fazla maaş almakta görülmektedir ve maaş dağılımı çok bariz şekilde çarpıktır. Çok küçük sayıda kişi (müdür ve 2 yardımcısı) karşılaştırılmalı olarak çok büyük değerde maaş almakta ama çok büyük sayıda kişi düşük değerde maaş almaktadır. Böylece maaş dağılımı gayet asimetrik olup sağda bir ince uzun bir kuyruk bulunmaktadır; veri dağılımı pozitif çarpıklık göstermektedir. Bu nedenle maaş aritmetik ortalaması merkezsel konum göstergesi olmaktan çıkmıştır.
Geometrik ortalama
Geometrik ortalama bir anakütle veya bir örneklem veri değerlerinin çarpımlarının o anakütledeki terim sayısına veya örneklem büyüklüğüne eşit kökü alınmak suretiyle elde edilen bir merkezsel konum değeridir. Bu tanımlama için formül şöyle verilir:

Burada G geometrik ortalama sembolüdür.
Bu tür ortalamanın da dezavantajları bulunmaktadır:
Mod veri dizisi içinde en çok defa tekrarlanan veri değeridir. Mod isimsel ölçekli veriler için anlamlı olan tek ortalama ölçüsüdür. Ancak veri dizisi içinde tek bir mod olmayabilir. Yahutta birden fazla sayıda mod bulunabilir.
Medyan
Medyan bir veri dizisinin küçükten büyüğe veya büyükten küçüğe sıralanmasından sonra bu dizinin tam ortasında bulunan değerdir. Eğer veri büyüklüğü tek sayılı ise medyan verilen bir veri değerine eşit olur. Eğer veri büyüklüğü çift sayılı ise medyan orta iki değerin ortalaması olur. Medyan bulmak için basit bir algoritmaya göre, sıralanmış veri değerlerinin kalan en küçük ve en büyük değerleri birer birer elimine edilir; veri sayısı tek ise en son kalan tek veri medyandır; eğer veri sayısı çift ise son kalan iki veri çiftinin ortalaması medyan olur.
Genelleştirilmiş ortalama türleri
İstatistikçiler ortalama türlerini genelleştiren tek bir formül bulmak için değişik yaklaşımlar kullanmışlardır:

Bu formülde m için değişik değerler değişik ortalama türü verirler: :

Burada f tersi alınabilir bir fonksiyondur. Bu formül değişik ortalamalar için şu şekilleri alır:
Değişik ortalama tipleri özeti
İstatistik bilim dalında bir sıra değişik ortalama tipleri geliştirilmiş ve bunlardan araştırıcının isteğine göre birinin veya bir kaçının eldeki veriler için merkezsel konum ölçüsü olarak kullanılması imkânı sağlanmıştır.

Sponsorlu Bağlantılar
Ortalama kavramı başlangiçta deniz nakliyatında ortaya çıkan zarar kavramından geliştirilmiştir. Deniz nakliyatinda zarar ya zarar gören esya sahibi tarafından özel avarya olarak tümüyle yüklenilir veya nakil edilen eşyaların satış kârını ortak olarak paylaşanlar tarafından genel avarya ortaklık payına göre olarak karşılanır. Genel avarya hesabının yapılması için geliştirilip kullanılan matematiksel hesaplar aritmetik ortalamanın ilk kullanılma alanı olmuştur. Bu kavrama Arapça avar, Italyanca avaria, Türkçe'de (pek çok denizcilik terimi gibi İtalyanca'dan alınan) avarya ve İngilizce average adı verilmektedir. İngilizce'de ayni sözcük, ve bazı günlük pratik hallerde Turkçe'de kullanılan avaraj sözcüğü ortalamaya eşit anlamda kullanılmaktadır.
Ortalama tipleri
Ortalama bir sayısal veri dizisininin merkezsel konumunu temsil etmek için seçilen tek bir sayı halinde bir özettir. Eğer veri dizisinde tüm elemanlar aynı sayı ise ortalama bu tek sayıdır. Ancak bu tip veri dizisi gayet nerede ise hiç bulunmadığı için değişik şekilde veri dizisinin merkezsel konumunu temsil edecek ortalamalar geliştirilmiştir. Önce bu ortalamalardan en çok kullanılanları kısaca ele alinacak ve sonra daha geniş kapsamlı bir tablo sunulacaktır.
En çok kullanılan ortalama tipleri
Aritmetik ortalama
Aritmetik ortalama bir anakütle veya bir örneklem veri değerlerinin toplamlarının o anakütledeki terim sayısına veya örneklem büyüklüğüne bölünerek elde edilen merkezsel konum değeridir. Bu tanınım şu formülle gösterilir:

Burada
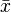 örneklem aritmetik ortalaması sembolüdür; anakütle aritmetik ortalaması için μ kullanılır.
örneklem aritmetik ortalaması sembolüdür; anakütle aritmetik ortalaması için μ kullanılır.İstatistikte sıkça kullanılır. Fakat bazı eksik yönleri vardır.
- Verilerin ölçülme ölçeğinin ya aralıklı veya oransal olması gerekir. İsimsel ölçekli veriler için aritmetik ortalama anlamsizdır. Birçok istatistikçi sırasal ölçekli veriler için aritmetik ortalamanın anlamsiz olduğunu kabul etmektedirler; ancak pratikte özellikle anketten ortaya çıkarılan sırasal ölçekli veriler için aritmetik ortalama hesaplanıp önemli alanlarda kullanılmaktadir.
- Eğer anakütle veya örneklem veri dağılımı simetrik olmayıp çarpıklık gösteriyorsa, aritmetik ortalama merkezsel değer olmaktan çıkıp çarpıklık kuyruğunun bulunduğu tarafa doğru gitmeye eğilimlidir. Bu istatistik bilenlerin, istatistik bilmeyenlere karşı kullanabilecekleri bir aldatmaca yolu da olabilir.
1 Genel Müdür: 15.000,00 YTL2 tane Genel Müdür Yardımcısı: her biri 5.500,00 YTL5 tane idari işler sorumluları (Halkla ilişkiler, İnsan kaynakları...vb): her biri 1.500,00 YTL30 tane normal personel = her biri 1.000,00 YTLBöyle bir durumda maaşların aritmetik ortalaması alınırsa
[15000+(3x5500)+(6x1500)+(30x1000)]/38 = 1671.05 YTL olarak ortalama aylık maaş hesaplanır. Ama bu ortalama merkezsel konumu göstermez. 38 personelden ancak 3u ortalamadan fazla maaş almakta görülmektedir ve maaş dağılımı çok bariz şekilde çarpıktır. Çok küçük sayıda kişi (müdür ve 2 yardımcısı) karşılaştırılmalı olarak çok büyük değerde maaş almakta ama çok büyük sayıda kişi düşük değerde maaş almaktadır. Böylece maaş dağılımı gayet asimetrik olup sağda bir ince uzun bir kuyruk bulunmaktadır; veri dağılımı pozitif çarpıklık göstermektedir. Bu nedenle maaş aritmetik ortalaması merkezsel konum göstergesi olmaktan çıkmıştır.
Geometrik ortalama
Geometrik ortalama bir anakütle veya bir örneklem veri değerlerinin çarpımlarının o anakütledeki terim sayısına veya örneklem büyüklüğüne eşit kökü alınmak suretiyle elde edilen bir merkezsel konum değeridir. Bu tanımlama için formül şöyle verilir:

Burada G geometrik ortalama sembolüdür.
Bu tür ortalamanın da dezavantajları bulunmaktadır:
- Büyük bir sayıda kök almak el hesabı ile imkânsız olduğu için bu tür ortalama genel olarak elektronik hesap makinelerinin veya kompüterlerin gelişmesinden önce kullanılması çok zor olmaktaydı. Verilerin logaritması alınıp; bu logaritma verilerinin toplamı bulunup; eldeki veri büyüklük sayısına bölünmesi ile geometrik ortalamaın logaritma değeri bulunup; bunun antilogaritmasının alınması gerekmekteydi. Orta basitlikte hesaplar yapabilen elektronik hesap makinaları veya kompüter kullanılarak geometrik ortalama almak çok kolaylaşmıştır.
- Geometrik ortalama bulabilmek için verilerin pozitif değerde olması gerekmektedir yani veri değerlerinin özellikle sıfır veya negatif olmaması gerekmektedir. Eğer tek bir veri değer sıfır ise, geometrik ortalama almak anlamsız olacaktır.
- Ayrıca verilerin ölçülme ölçeğinin oransal olması gerekir; isimsel ölçekli, sırasal ölçekli ve aralıksal ölçekli veri değerleri için geometrik ortalama anlamsız olur.
Mod veri dizisi içinde en çok defa tekrarlanan veri değeridir. Mod isimsel ölçekli veriler için anlamlı olan tek ortalama ölçüsüdür. Ancak veri dizisi içinde tek bir mod olmayabilir. Yahutta birden fazla sayıda mod bulunabilir.
Medyan
Medyan bir veri dizisinin küçükten büyüğe veya büyükten küçüğe sıralanmasından sonra bu dizinin tam ortasında bulunan değerdir. Eğer veri büyüklüğü tek sayılı ise medyan verilen bir veri değerine eşit olur. Eğer veri büyüklüğü çift sayılı ise medyan orta iki değerin ortalaması olur. Medyan bulmak için basit bir algoritmaya göre, sıralanmış veri değerlerinin kalan en küçük ve en büyük değerleri birer birer elimine edilir; veri sayısı tek ise en son kalan tek veri medyandır; eğer veri sayısı çift ise son kalan iki veri çiftinin ortalaması medyan olur.
Genelleştirilmiş ortalama türleri
İstatistikçiler ortalama türlerini genelleştiren tek bir formül bulmak için değişik yaklaşımlar kullanmışlardır:
- Genelleştirilmiş ortalama formülü şöyle verilir:

Bu formülde m için değişik değerler değişik ortalama türü verirler: :
- eğer m = 1 ise aritmetik ortalama;
- eğer m = 2 ise kuadratik ortalama;
- eğer m = -1 ise harmonik ortalama;
- limit m → 0 ise
 geometrik ortalamaya yaklaşır.
geometrik ortalamaya yaklaşır.
- Genelleştirilmiş f-ortalaması formülü diğer bir örnektir. Genelleştirilmiş f-ortalaması için formül şudur:

Burada f tersi alınabilir bir fonksiyondur. Bu formül değişik ortalamalar için şu şekilleri alır:
- Geometrik ortalama için f(x)=log x olur.
- Harmonik ortalama için f(x)= 1/x olur.
- Çok az bilinen üstel ortalama için f(x)=ex olur.
- Diğer bir genelleştirme, ortalamalar listesi elamanlarının permütasyonu halinde simetrik olan bir g(x1, x2, ..., xn) fonksiyonunun değişik şekillerde ifadesi ile yapılır:
- Aritmetik ortalama için g(x1, x2, ..., xn) =x1+x2+ ...+ xn.
- Geometrik ortalama için g(x1, x2, ..., xn) =x1·x2· ...· xn.
- Harmonik ortalama için g(x1, x2, ..., xn) =x1−1+x2−1+ ...+ xn−1.
Değişik ortalama tipleri özeti
İstatistik bilim dalında bir sıra değişik ortalama tipleri geliştirilmiş ve bunlardan araştırıcının isteğine göre birinin veya bir kaçının eldeki veriler için merkezsel konum ölçüsü olarak kullanılması imkânı sağlanmıştır.


 Ortalama
Ortalama
